题目内容
已知以下四个命题:
①如果x1,x2是一元二次方程ax2+bx+c=0的两个实根,且x1<x2,那么不等式ax2+bx+c<0的解集为
{x|x1<x<x2;
②“若m>2,则x2-2x+m>0的解集是实数集R”的逆否命题;
③若 x-1x-2≤0,则(x-1)(x-2)≤0.
④直线y=1与曲线y=x2-|x|+a有四个交点,则a的取值范围是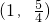
其中为真命题的是________(填上你认为正确的序号)
②④
分析:根据二次不等式的解法,可以判断①的真假;根据四种命题真假性的关系,可以判断②的正误;由分式不等式的解法,可以判断③的对错;根据函数的奇偶性,可以判断④的真假,进而得到答案.
解答:①当a>0时,不等式ax2+bx+c<0的解集为{x|x1<x<x2};
当a<0时,不等式ax2+bx+c<0的解集为{x|x<x1,或x>x2}.故①不成立.
②∵若m>2,则x2-2x+m>0的解集是实数集R为真命题,∴“若m>2,则x2-2x+m>0的解集是实数集R”的逆否命题也为真命题,故②成立;
③若 ,则(x-1)(x-2)≤0且x-2≠0,故③错误;
,则(x-1)(x-2)≤0且x-2≠0,故③错误;
④y=|x|2-|x|+a是个偶函数,图象关于y轴对称,
当x≥0时,y=x2-x+a,对称轴 x= ,
,
在(0, ),y∈(
),y∈( ,a)
,a)
在( ,+∞),y∈(-∞,
,+∞),y∈(-∞, )
)
由此知当 时,直线y=1与曲线y=x2-|x|+a有四个交点,
时,直线y=1与曲线y=x2-|x|+a有四个交点,
解得1<a< .故④成立.
.故④成立.
故答案为:②④.
点评:本题考查的知识点是命题的真假判断与应用,命题的否定,函数的周期性及一元二次不等式的解法,直接考查了这些知识的基本应用,属于基础题.
分析:根据二次不等式的解法,可以判断①的真假;根据四种命题真假性的关系,可以判断②的正误;由分式不等式的解法,可以判断③的对错;根据函数的奇偶性,可以判断④的真假,进而得到答案.
解答:①当a>0时,不等式ax2+bx+c<0的解集为{x|x1<x<x2};
当a<0时,不等式ax2+bx+c<0的解集为{x|x<x1,或x>x2}.故①不成立.
②∵若m>2,则x2-2x+m>0的解集是实数集R为真命题,∴“若m>2,则x2-2x+m>0的解集是实数集R”的逆否命题也为真命题,故②成立;
③若
 ,则(x-1)(x-2)≤0且x-2≠0,故③错误;
,则(x-1)(x-2)≤0且x-2≠0,故③错误;④y=|x|2-|x|+a是个偶函数,图象关于y轴对称,
当x≥0时,y=x2-x+a,对称轴 x=
 ,
,在(0,
 ),y∈(
),y∈( ,a)
,a)在(
 ,+∞),y∈(-∞,
,+∞),y∈(-∞, )
)由此知当
 时,直线y=1与曲线y=x2-|x|+a有四个交点,
时,直线y=1与曲线y=x2-|x|+a有四个交点,解得1<a<
 .故④成立.
.故④成立.故答案为:②④.
点评:本题考查的知识点是命题的真假判断与应用,命题的否定,函数的周期性及一元二次不等式的解法,直接考查了这些知识的基本应用,属于基础题.

练习册系列答案
相关题目