题目内容
(本小题满分12分)已知直线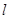 的参数方程为
的参数方程为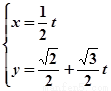 (
(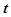 为参数),若以直角坐标系
为参数),若以直角坐标系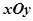 的
的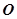 点为极点,
点为极点,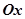 方向为极轴,选择相同的长度单位建立极坐标系,得曲线
方向为极轴,选择相同的长度单位建立极坐标系,得曲线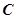 的极坐标方程为
的极坐标方程为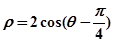
(1)将直线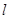 的参数方程化为普通方程,把曲线
的参数方程化为普通方程,把曲线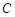 的极坐标方程化为直角坐标方程;
的极坐标方程化为直角坐标方程;
(2)若直线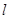 与曲线
与曲线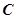 交于
交于 两点,求
两点,求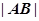 .
.
【答案】
(1)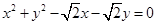 ;
;
(2) ,
,  。
。
【解析】本题考查把极坐标方程化为直角坐标方程的方法,直线的参数方程中参数的几何意义,是一道基础题
(1)消去参数可得直线l的普通方程,曲线C的方程可化为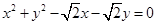
(2)由上知配方,得圆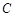 的标准方程为
的标准方程为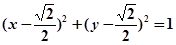
那么利用圆心到直线的距离公式,结合勾股定理得到弦长的求解。
解:(1)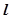 的直角坐标方程为
的直角坐标方程为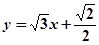 ,(或
,(或 )..(2分)
)..(2分)
曲线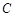 的直角坐标方程为
的直角坐标方程为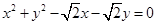 ………………………(5分)
………………………(5分)
(2)配方,得圆 的标准方程为
的标准方程为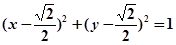
知圆心 ,半径
,半径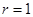 ,
,
所以圆心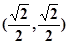 到直线
到直线 的距离
的距离 ,……(9分)
,……(9分)
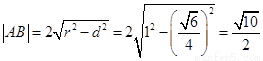 ……………………………(12分)
……………………………(12分)
(注:可用弦长公式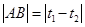 求解,酌情给分)
求解,酌情给分)

练习册系列答案
相关题目