题目内容
已知点(1,1)是椭圆
+
=1某条弦的中点,则此弦所在的直线方程为:
| x2 |
| 4 |
| y2 |
| 2 |
x+2y-3=0
x+2y-3=0
.分析:设以A(1,1)为中点椭圆的弦与椭圆交于E(x1,y1),F(x2,y2),A(1,1)为EF中点,x1+x2=2,y1+y2=2,利用点差法能够求出以A(1,1)为中点椭圆的弦所在的直线方程.
解答:解:设以A(1,1)为中点椭圆的弦与椭圆交于E(x1,y1),F(x2,y2),
∵A(1,1)为EF中点,
∴x1+x2=2,y1+y2=2,
把E(x1,y1),F(x2,y2)分别代入椭圆
+
=1,
可得
+
=1,
+
=1
两式相减,可得(x1+x2)(x1-x2)+2(y1+y2)(y1-y2)=0,
∴2(x1-x2)+4(y1-y2)=0,
∴k=
=-
∴以A(1,1)为中点椭圆的弦所在的直线方程为:y-1=-
(x-1),
整理,得x+2y-3=0.
故答案为:x+2y-3=0.
∵A(1,1)为EF中点,
∴x1+x2=2,y1+y2=2,
把E(x1,y1),F(x2,y2)分别代入椭圆
| x2 |
| 4 |
| y2 |
| 2 |
可得
| x12 |
| 4 |
| y12 |
| 2 |
| x22 |
| 4 |
| y22 |
| 2 |
两式相减,可得(x1+x2)(x1-x2)+2(y1+y2)(y1-y2)=0,
∴2(x1-x2)+4(y1-y2)=0,
∴k=
| y1-y2 |
| x1-x2 |
| 1 |
| 2 |
∴以A(1,1)为中点椭圆的弦所在的直线方程为:y-1=-
| 1 |
| 2 |
整理,得x+2y-3=0.
故答案为:x+2y-3=0.
点评:本题考查以A(1,1)为中点椭圆的弦所在的直线方程的求法,考查点差法的运用,考查学生分析解决问题的能力,属于中档题.

练习册系列答案
相关题目


 +
+ =1左准线上一点,F1、F2分别是其左、右焦点,PF2与椭圆交于点Q,且
=1左准线上一点,F1、F2分别是其左、右焦点,PF2与椭圆交于点Q,且 =2
=2 ,则|
,则| |的值为( )
|的值为( )


 +
+ =1左准线上一点,F1、F2分别是其左、右焦点,PF2与椭圆交于点Q,且
=1左准线上一点,F1、F2分别是其左、右焦点,PF2与椭圆交于点Q,且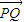 =2
=2 ,则|
,则| |的值为( )
|的值为( )

