题目内容
如图,四边形OABC为矩形,点A、C的坐标分别为(a+1,0)(a>1)、(0,1),点D在OA上,坐标为(a,0),椭圆C分别以OD、OC为长、短半轴,CD是椭圆在矩形内部的椭圆弧.已知直线l:y=-x+m与椭圆弧相切,且与AD相交于点E.
(Ⅰ)当m=2时,求椭圆C的标准方程;
(Ⅱ)圆M在矩形内部,且与l和线段EA都相切,若直线l将矩形OABC分成面积相等的两部分,求圆M面积的最大值.

【答案】分析:(1)设椭圆的方程为 .由
.由 得(1+a2)x2-2a2mx+a2(m2-1)=0.由于直线l与椭圆相切,知△=(2a2m)2-4(1+a2)a2(m2-1)=0,由此能求出椭圆C的标准方程.
得(1+a2)x2-2a2mx+a2(m2-1)=0.由于直线l与椭圆相切,知△=(2a2m)2-4(1+a2)a2(m2-1)=0,由此能求出椭圆C的标准方程.
(2)由题意知A(a+1,0),B(a+1,1),C(0,1),于是OB的中点为 .因为l将矩形OABC分成面积相等的两部分,所以l过点
.因为l将矩形OABC分成面积相等的两部分,所以l过点 ,由此入手,能够求出圆M面积的最大值.
,由此入手,能够求出圆M面积的最大值.
解答:解:(1)设椭圆的方程为 .k•s5•u
.k•s5•u
由 消去y得(1+a2)x2-2a2mx+a2(m2-1)=0.(3分)
消去y得(1+a2)x2-2a2mx+a2(m2-1)=0.(3分)
由于直线l与椭圆相切,∴△=(2a2m)2-4(1+a2)a2(m2-1)=0,
化简得m2-a2=1,①
当m=2时,a2=3,
则椭圆C的标准方程为 .(6分)
.(6分)
(2)由题意知A(a+1,0),B(a+1,1),C(0,1),于是OB的中点为 .
.
因为l将矩形OABC分成面积相等的两部分,所以l过点 ,
,
即 ,亦即2m-a=2.②
,亦即2m-a=2.②
由①②解得 ,故直线l的方程为
,故直线l的方程为 .(9分)
.(9分)
∴ .
.
因为圆M与线段EA相切,所以可设其方程为(x-x)2+(y-r)2=r2(r>0).
因为圆M在矩形及其内部,所以 ④
④
圆M与l相切,且圆M在l上方,所以 ,即
,即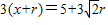 .
.
代入④得 即
即 .
.
所以圆M面积最大时, ,这时,圆M面积的最大值为
,这时,圆M面积的最大值为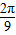 .(15分)
.(15分)
点评:本题主要考查直线与圆锥曲线的综合应用能力,具体涉及到轨迹方程的求法及直线与椭圆的相关知识,解题时要注意合理地进行等价转化.
 .由
.由 得(1+a2)x2-2a2mx+a2(m2-1)=0.由于直线l与椭圆相切,知△=(2a2m)2-4(1+a2)a2(m2-1)=0,由此能求出椭圆C的标准方程.
得(1+a2)x2-2a2mx+a2(m2-1)=0.由于直线l与椭圆相切,知△=(2a2m)2-4(1+a2)a2(m2-1)=0,由此能求出椭圆C的标准方程.(2)由题意知A(a+1,0),B(a+1,1),C(0,1),于是OB的中点为
 .因为l将矩形OABC分成面积相等的两部分,所以l过点
.因为l将矩形OABC分成面积相等的两部分,所以l过点 ,由此入手,能够求出圆M面积的最大值.
,由此入手,能够求出圆M面积的最大值.解答:解:(1)设椭圆的方程为
 .k•s5•u
.k•s5•u由
 消去y得(1+a2)x2-2a2mx+a2(m2-1)=0.(3分)
消去y得(1+a2)x2-2a2mx+a2(m2-1)=0.(3分)由于直线l与椭圆相切,∴△=(2a2m)2-4(1+a2)a2(m2-1)=0,
化简得m2-a2=1,①
当m=2时,a2=3,
则椭圆C的标准方程为
 .(6分)
.(6分)(2)由题意知A(a+1,0),B(a+1,1),C(0,1),于是OB的中点为
 .
.因为l将矩形OABC分成面积相等的两部分,所以l过点
 ,
,即
 ,亦即2m-a=2.②
,亦即2m-a=2.②由①②解得
 ,故直线l的方程为
,故直线l的方程为 .(9分)
.(9分)∴
 .
.因为圆M与线段EA相切,所以可设其方程为(x-x)2+(y-r)2=r2(r>0).
因为圆M在矩形及其内部,所以
 ④
④圆M与l相切,且圆M在l上方,所以
 ,即
,即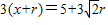 .
.代入④得
 即
即 .
.所以圆M面积最大时,
 ,这时,圆M面积的最大值为
,这时,圆M面积的最大值为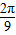 .(15分)
.(15分)点评:本题主要考查直线与圆锥曲线的综合应用能力,具体涉及到轨迹方程的求法及直线与椭圆的相关知识,解题时要注意合理地进行等价转化.

练习册系列答案
相关题目

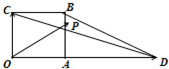 如图,四边形OABC是边长为1的正方形,OD=3,点P为△BCD内(含边界)的动点,设
如图,四边形OABC是边长为1的正方形,OD=3,点P为△BCD内(含边界)的动点,设 如图,四边形OABC是面积为4的正方形,函数
如图,四边形OABC是面积为4的正方形,函数 (2013•文昌模拟)如图,四边形OABC是边长为1的正方形,OD=3,点P为△BCD内(含边界)的动点,设
(2013•文昌模拟)如图,四边形OABC是边长为1的正方形,OD=3,点P为△BCD内(含边界)的动点,设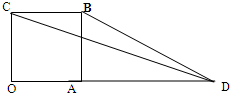 如图,四边形OABC是边长为1的正方形,
如图,四边形OABC是边长为1的正方形,