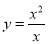题目内容
6.(x+$\frac{2}{x}$)(1-x)4的展开式中,x3项的系数是8.分析 将问题转化为二项式(1-x)4的展开式的系数问题,求出(1-x)4展开式的通项,分别令r=4,2求出展开式中x3项的系数.
解答 解:(x+$\frac{2}{x}$)(1-x)4的展开式中x3项的系数是(1-x)4展开式中x4项的系数的2倍与(1-x)4展开式中x2项的系数的和
∵(1-x)4展开式的通项为Tr+1=(-1)rC4rxr
令r=4得到x4项的系数为1;令r=2得到x2项的系数为C42=6
∴(x+$\frac{2}{x}$)(1-x)4的展开式中x3项的系数是2+6=8,
故答案为:8.
点评 解决二项展开式的特定项问题常利用的工具是二项展开式的通项公式.

练习册系列答案
相关题目
 与
与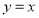 B.
B.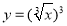 与
与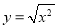 与
与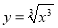 与
与