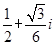题目内容
已知a,b∈R,i是虚数单位.若(a+i)(1+i)=bi,则a+bi=________.
1+2i
由复数相等的定义求得a,b的值,即得复数.
由(a+i)(1+i)=bi可得(a-1)+(a+1)i=bi,因此a-1=0,a+1=b,解得a=1,b=2,故a+bi=1+2i.
由(a+i)(1+i)=bi可得(a-1)+(a+1)i=bi,因此a-1=0,a+1=b,解得a=1,b=2,故a+bi=1+2i.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
 =1,则sin2θ= .
=1,则sin2θ= . =3-4i(i为虚数单位),则|z|=________.
=3-4i(i为虚数单位),则|z|=________. 为虚数单位,且
为虚数单位,且 ,则
,则 的值是( )
的值是( ) 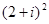 = ( )
= ( )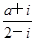 是纯虚数,则实数a=( ).
是纯虚数,则实数a=( ).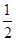
 满足
满足 ,则
,则




 =( ).
=( ).