题目内容
解关于x的方程
①x2+2x+3=0;②x2+6x+13=0.
①x2+2x+3=0;②x2+6x+13=0.
①x=-1+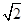 i或x=-1-
i或x=-1-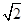 i②x=-3+2i或x=-3-2i
i②x=-3+2i或x=-3-2i
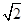 i或x=-1-
i或x=-1-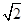 i②x=-3+2i或x=-3-2i
i②x=-3+2i或x=-3-2i①设x=a+bi(a,b∈R),
则x2+2x+3=a2-b2+2abi+2a+2bi+3
=(a2-b2+2a+3)+(2ab+2b)i=0.
∵a,b∈R,∴a2-b2+2a+3=0且2ab+2b=0.
∴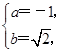 或
或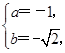 ∴x=-1+
∴x=-1+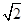 i或x=-1-
i或x=-1-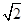 i
i
②设x=a+bi(a,b∈R),
则x2+6x+13=a2-b2+2abi+6a+6bi+13
=a2-b2+6a+13+(2ab+6b)i=0.
∵a,b∈R,∴a2-b2+6a+13=0且2ab+6b=0.
∴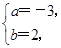 或
或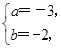 ∴x=-3+2i或x=-3-2i
∴x=-3+2i或x=-3-2i
则x2+2x+3=a2-b2+2abi+2a+2bi+3
=(a2-b2+2a+3)+(2ab+2b)i=0.
∵a,b∈R,∴a2-b2+2a+3=0且2ab+2b=0.
∴
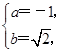 或
或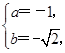 ∴x=-1+
∴x=-1+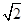 i或x=-1-
i或x=-1-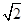 i
i②设x=a+bi(a,b∈R),
则x2+6x+13=a2-b2+2abi+6a+6bi+13
=a2-b2+6a+13+(2ab+6b)i=0.
∵a,b∈R,∴a2-b2+6a+13=0且2ab+6b=0.
∴
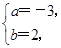 或
或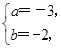 ∴x=-3+2i或x=-3-2i
∴x=-3+2i或x=-3-2i
练习册系列答案
相关题目
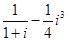 对应的点位于 )
对应的点位于 ) (为虚数单位)的共轭复数对应的点位于第__________象限.
(为虚数单位)的共轭复数对应的点位于第__________象限. =(a+2z)2.
=(a+2z)2.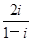 对应点的坐标为________,复数的模为________.
对应点的坐标为________,复数的模为________. =( )
=( ) i
i 的虚部是( )
的虚部是( )