题目内容
设
是定义在
上的奇函数，且
的图像关于直线
对称，则
= ．
0
解析试题分析：的图像关于直线对称，所以
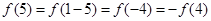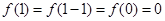，又是定义在上的奇函数，所以
，
，
，所以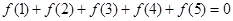
.
考点：函数图象的中心对称和轴对称.
练习册系列答案
相关题目
题目内容
设是定义在上的奇函数，且的图像关于直线对称，则= ．
0
解析试题分析：的图像关于直线对称，所以，又是定义在上的奇函数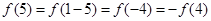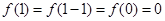，所以，，，所以.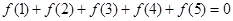
考点：函数图象的中心对称和轴对称.
与
，则关于
与
的下列说法正确的是 .
为偶函数；
，则 
.
的图象与直线
有两个公共点，则
的取值范围是____.
与
的图象的交点为
，且
，则
= .
时，则下列结论正确的是 .
，等式
恒成立
，使得方程
有两个不等实数根
，若
，则一定有
，使得函数
在
上有三个零点
，使
成立，则实数
的取值范围是 .
上的偶函数
的周期为2，且当
时，
，则
.