题目内容
(本小题满分12分)
如图,已知在坐标平面xOy内,M、N是x轴上关于原点O对称的两点,P是上半平面内一点,△PMN的面积为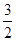 ,点A的坐标为(1+
,点A的坐标为(1+ ),
),  =m·
=m·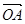 (m为常数),
(m为常数),



(1)求以M、N为焦点且过点P的椭圆方程;
(2)过点B(-1,0)的直线l交椭圆于C、D两点,交直线x=-4于点E,点B、E分 的比分别为λ1、λ2,求λ1+λ2的值。
的比分别为λ1、λ2,求λ1+λ2的值。
解:(1)设M(-c,0),N(c,0)(c>0),P(x0,y0),则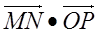 =(2c,0)·(x0,y0)=2cx0,
=(2c,0)·(x0,y0)=2cx0,
2cx0=2c,故x0=1. ①
又∵S△PMN=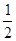 (2c)|y0|=
(2c)|y0|=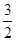 ,y0=
,y0=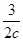 .
②
.
②
∵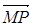 =(x0+c,y0),
=(x0+c,y0),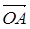 =(1+
=(1+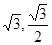 ),由已知(x0+c,y0)=m(1+
),由已知(x0+c,y0)=m(1+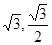 ),即
),即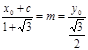 .
.
故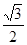 (x0+c)=(1+
(x0+c)=(1+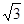 )y0. ③
)y0. ③
将①②代入③,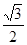 (1+c)=(1+
(1+c)=(1+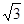 )·
)·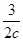 ,c2+c-(3+
,c2+c-(3+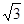 )=0,(c-
)=0,(c-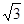 )(c+
)(c+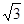 +1)=0,
+1)=0,
∴c=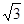 ,y0=
,y0=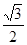 .
.
设椭圆方程为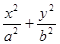 =1(a>b>0).
=1(a>b>0).
∵a2=b2+3,P(1,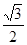 )在椭圆上,
)在椭圆上,
∴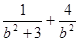 =1.故b2=1,a2=4.
=1.故b2=1,a2=4.
∴椭圆方程为 +y2=1.
6分
+y2=1.
6分
(2)①当l的斜率不存在时,l与x=-4无交点,不合题意.
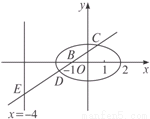
②当l的斜率存在时,设l方程为y=k(x+1),
代入椭圆方程 +y2=1,
+y2=1,
化简得(4k2+1)x2+8k2x+4k2-4=0. 8分
设点C(x1,y1)、D(x2,y2),则
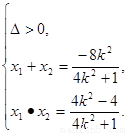
∵-1=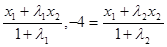 ,
,
∴λ1=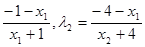 .
9分
.
9分
λ1+λ2=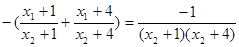 [2x1x2+5(x1+x2)+8],
[2x1x2+5(x1+x2)+8],
而2x1x2+5(x1+x2)+8=2·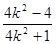 +5·
+5·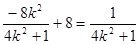 (8k2-8-40k2+32k2+8)=0,
(8k2-8-40k2+32k2+8)=0,
∴λ1+λ2=0. 12分
22、(文)解:(1)当n≥2时,an=Sn-Sn-1=2an-4-2an-1+4,
即得an=2an-1,
当n=1时,a1=S1=2a1-4=4,∴an=2n+1. 3分
∴bn+1=2n+1+2bn.∴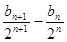 =1.
=1.
∴{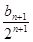 }是以1为首项,以1为公差的等差数列.
}是以1为首项,以1为公差的等差数列.
∴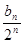 =1+(n-1)×1=n∴bn=n·2n.
6分
=1+(n-1)×1=n∴bn=n·2n.
6分
(2)Tn=1·2+2·22+…+n·2n, ①
2Tn=1·22+2·23+…+(n-1)·2n+n·2n+1, ②
①-②,得-Tn=2+22+23+…+2n-n·2n+1=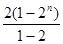 n·2n+1,
n·2n+1,
∴Tn=(n-1)·2n+1+2. 12分
【解析】略

 名校课堂系列答案
名校课堂系列答案