题目内容
在Rt△ACB中,∠C=90°,CD⊥AB于D,若BD∶AD=1∶4,则tan∠BCD的值是
A.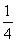 B.
B.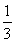 C.
C.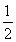 D.2
D.2
C
【解析】如图所示,由射影定理得
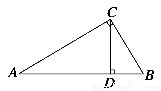
CD2=AD·BD,
又∵BD∶AD=1∶4,令BD=x,则AD=4x (x>0).
∴CD2=AD·BD=4x2,∴CD=2x,
在Rt△CDB中,tan∠BCD=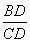 =
=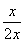 =
=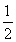 .
.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
题目内容
在Rt△ACB中,∠C=90°,CD⊥AB于D,若BD∶AD=1∶4,则tan∠BCD的值是
A.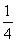 B.
B.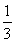 C.
C.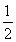 D.2
D.2
C
【解析】如图所示,由射影定理得

CD2=AD·BD,
又∵BD∶AD=1∶4,令BD=x,则AD=4x (x>0).
∴CD2=AD·BD=4x2,∴CD=2x,
在Rt△CDB中,tan∠BCD=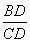 =
=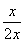 =
=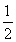 .
.

 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案