Question

已知平面区域D是由以A（2，4）、B（-1，2）、C（1，0）为顶点的三角形内部和边界组成，若在区域D上有无穷多个点（x，y）可使z=x-ay取最大值，则a=

1

4

．

Answer 1

分析：先将目标函数z=x-ay化成斜截式方程后得：y=

1

a

x-

1

a

z，目标函数值-

1

a

z是直线族y=

1

a

x-

1

a

z的截距，当直线族y=

1

a

x-

1

a

z的斜率与直线AC的斜率相等时，目标函数z=x-ay取得最大值的最优解有无数多个，由此不难得到a的值．

解答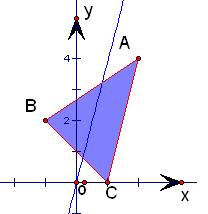：解：∵目标函数z=x-ay，
∴y=

1

a

x-

1

a

z，
故目标函数值-

1

a

z是直线族y=

1

a

x-

1

a

z的截距
当直线族y=

1

a

x-

1

a

z的斜率与直线AC的斜率相等时，
目标函数z=x-ay取得最大值的最优解有无数多个
此时

1

a

=

0-4

1-2

=4
即a=

1

4

故答案为：

1

4

．

点评：目标函数的最优解有无数多个，处理方法一般是：①将目标函数的解析式进行变形，化成斜截式②分析Z与截距的关系，是符号相同，还是相反③根据分析结果，结合图形做出结论④根据斜率相等求出参数．