题目内容

（2009•枣庄一模）如果函数f（x）=ax+b-1（a＞0且a≠1）的图象经过第一、二、四象限，不经过第三象限，那么一定有（　　）
分析：利用指数函数的图象判断a，b的取值范围．
解答：解：因为函数f（x）=ax+b-1（a＞0且a≠1）的图象经过第一、二、四象限，不经过第三象限，
则根据指数函数的图象可知，0＜a＜1，当x=0时，0＜y＜1，
即0＜1+b-1＜1，解得0＜b＜1．
故选B．
点评：本题主要考查了指数函数的图象和性质，要求熟练掌握指数函数的图象与性质．
练习册系列答案
相关题目
（2009•枣庄一模）已知数列{an}的各项均是正数，其前n项和为Sn，满足（p-1）Sn=p2-an，其中p为正常数，且p≠1．
（1）求数列{an}的通项公式；
（2）设bn=
12-logpan
(n∈N*)，求数列{bnbn+1}的前n项和Tn的取值范围；
（3）是否存在正整数M，使得n＞M时，a1a4a7…a3n-2＞a78恒成立？若存在，求出相应的M的最小值；若不存在，请说明理由．
（2009•枣庄一模）设(5x-
1
x
)n的展开式的各项系数和为M，二项式系数和为N，若M-N=240，则展开式中x的系数为（　　）
（2009•枣庄一模）先后抛掷两枚骰子，每次各1枚，求下列事件发生的概率：
（1）事件A：“出现的点数之和大于3”；
（2）事件B：“出现的点数之积是3的倍数”．
（2009•枣庄一模）设复数z的共轭复数是
.
z
，若复数z1=3+4i，z2=t+i，且z1•
.
z2
是实数，则实数t=（　　）
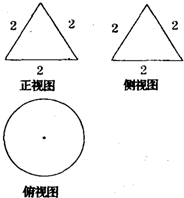（2009•枣庄一模）一个几何体的三视图如图所示，则该几何体外接球的表面积为（　　）

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网