题目内容
(2012•黄冈模拟)已知椭圆
+
=1(a>b>0)的离心率为
,椭圆上任意一点到右焦点F的距离的最大值为
+1.
(I)求椭圆的方程;
(Ⅱ)已知点C(m,0)是线段OF上一个动点(O为坐标原点),是否存在过点F且与x轴不垂直的直线l与椭圆交于A、B两点,使得|AC|=|BC|,并说明理由.
| x2 |
| a2 |
| y2 |
| b2 |
| ||
| 2 |
| 2 |
(I)求椭圆的方程;
(Ⅱ)已知点C(m,0)是线段OF上一个动点(O为坐标原点),是否存在过点F且与x轴不垂直的直线l与椭圆交于A、B两点,使得|AC|=|BC|,并说明理由.
分析:(1)结合已知
,可求a,c,由b2=a2-c2可求b,进而可求椭圆方程
(2)由题意可知0≤m<1,假设存在满足题意的直线l,设l的方程为y=k(x-1),代入
+y2=1,设A(x1,y1),B(x2,y2),根据方程的根与系数关系可求x1+x2,x1x2,根据y1+y2=k(x1+x2-2),从而可求B的中点为M,由|AC|=|BC|可得kCM•kAB=-1可得m,k之间得关系,结合m的范围可求k
|
(2)由题意可知0≤m<1,假设存在满足题意的直线l,设l的方程为y=k(x-1),代入
| x2 |
| 2 |
解答:解:(1)因为
,所以a=
,c=1,(4分)
∴b=1,椭圆方程为:
+y2=1 (6分)
(2)由(1)得F(1,0),所以0≤m<1,假设存在满足题意的直线l,设l的方程为y=k(x-1),
代入
+y2=1,得(1+2k2)x2-4k2x+2k2-2=0
设A(x1,y1),B(x2,y2),则x1+x2=
,x1x2=
①,(10分)
y1+y2=k(x1+x2-2)=
设AB的中点为M,则M(
,
),
∵|AC|=|BC|
∴CM⊥AB即kCM•kAB=-1
∴
-2m+
•k=0
∴(1-2m)k2=m
∴当0≤m<
时,k=±
,即存在这样的直线l
当
≤m≤1,k不存在,即不存在这样的直线l (15分)
|
| 2 |
∴b=1,椭圆方程为:
| x2 |
| 2 |
(2)由(1)得F(1,0),所以0≤m<1,假设存在满足题意的直线l,设l的方程为y=k(x-1),
代入
| x2 |
| 2 |
设A(x1,y1),B(x2,y2),则x1+x2=
| 4k2 |
| 1+2k2 |
| 2k2-2 |
| 2k2+1 |
y1+y2=k(x1+x2-2)=
| -2k |
| 2k2+1 |
设AB的中点为M,则M(
| 2k2 |
| 2k2+1 |
| -k |
| 2k2+1 |
∵|AC|=|BC|
∴CM⊥AB即kCM•kAB=-1
∴
| 4k2 |
| 1+2k2 |
| -2k |
| 2k2+1 |
∴(1-2m)k2=m
∴当0≤m<
| 1 |
| 2 |
|
当
| 1 |
| 2 |
点评:本题主要考查了利用椭圆的性质求解椭圆的方程,直线与椭圆相交关系的应用,方程的根与系数关系的应用,直线的斜率公式的应用.属于知识的综合应用.

练习册系列答案
相关题目
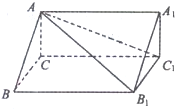 (2012•黄冈模拟)如图,三棱柱ABC-A1B1C1中,AA1⊥平面ABC,AA1=
(2012•黄冈模拟)如图,三棱柱ABC-A1B1C1中,AA1⊥平面ABC,AA1=