题目内容
如图,在平面直角坐标系xoy中,角α的始边与x轴的非负半轴重合且与单位圆相交于A点,它的终边与单位圆相交于x轴上方一点B,始边不动,终边在运动.
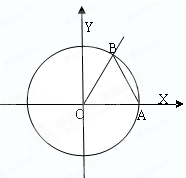
(1)若点B的横坐标为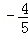 ,求tanα的值;
,求tanα的值;
(2)若△AOB为等边三角形,写出与角α终边相同的角β的集合;
(3)若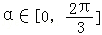 ,请写出弓形AB的面积S与α的函数关系式,并指出函数的值域.
,请写出弓形AB的面积S与α的函数关系式,并指出函数的值域.

(1)若点B的横坐标为
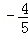 ,求tanα的值;
,求tanα的值;(2)若△AOB为等边三角形,写出与角α终边相同的角β的集合;
(3)若
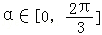 ,请写出弓形AB的面积S与α的函数关系式,并指出函数的值域.
,请写出弓形AB的面积S与α的函数关系式,并指出函数的值域.(1)﹣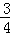
(2){β|β=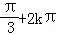 ,k∈Z}∪{β|β=
,k∈Z}∪{β|β=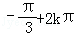 ,k∈Z}
,k∈Z}
(3)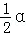 ﹣
﹣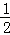 sinα,
sinα,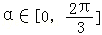 值域为:[0,
值域为:[0, ]
]
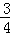
(2){β|β=
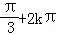 ,k∈Z}∪{β|β=
,k∈Z}∪{β|β=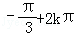 ,k∈Z}
,k∈Z}(3)
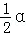 ﹣
﹣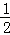 sinα,
sinα,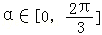 值域为:[0,
值域为:[0, ]
](1)由题意可得B(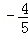 ,
,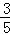 ),根据三角函数的定义得;
),根据三角函数的定义得;
(2)同理可得B的坐标,注意两种情况,然后由三角函数的定义可得;
(3)把弓形转化为扇形和三角形的面积之差,由导数可得函数的单调性,进而可得值域.
(1)由题意可得B(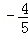 ,
,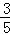 ),根据三角函数的定义得:tanα=
),根据三角函数的定义得:tanα= =﹣
=﹣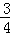 ;
;
(2)若△AOB为等边三角形,则B( ,
,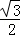 )或(
)或( ,
, )
)
可得tan∠AOB=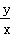 =
=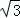 或
或 ,故∠AOB=
,故∠AOB=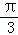 ,或
,或 ;
;
故与角α终边相同的角β的集合为:{β|β=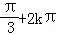 ,k∈Z}∪{β|β=
,k∈Z}∪{β|β=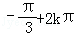 ,k∈Z};
,k∈Z};
(3)若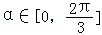 ,则S扇形=
,则S扇形= αr2=
αr2=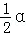 ,而S△AOB=
,而S△AOB= ×1×1×sinα=
×1×1×sinα= sinα,
sinα,
故弓形的面积S=S扇形﹣S△AOB=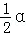 ﹣
﹣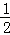 sinα,
sinα,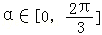 ,
,
求导数可得S′=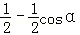 =
=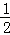 (1﹣cosα)>0,故S在区间
(1﹣cosα)>0,故S在区间 上单调递增,
上单调递增,
S(0)=0,S(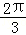 )=
)= ,
,
故函数的值域为:[0, ]
]
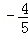 ,
,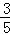 ),根据三角函数的定义得;
),根据三角函数的定义得;(2)同理可得B的坐标,注意两种情况,然后由三角函数的定义可得;
(3)把弓形转化为扇形和三角形的面积之差,由导数可得函数的单调性,进而可得值域.
(1)由题意可得B(
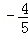 ,
,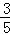 ),根据三角函数的定义得:tanα=
),根据三角函数的定义得:tanα= =﹣
=﹣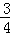 ;
;(2)若△AOB为等边三角形,则B(
 ,
,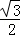 )或(
)或( ,
, )
)可得tan∠AOB=
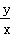 =
=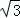 或
或 ,故∠AOB=
,故∠AOB=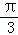 ,或
,或 ;
;故与角α终边相同的角β的集合为:{β|β=
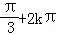 ,k∈Z}∪{β|β=
,k∈Z}∪{β|β=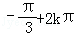 ,k∈Z};
,k∈Z};(3)若
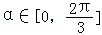 ,则S扇形=
,则S扇形= αr2=
αr2=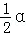 ,而S△AOB=
,而S△AOB= ×1×1×sinα=
×1×1×sinα= sinα,
sinα,故弓形的面积S=S扇形﹣S△AOB=
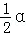 ﹣
﹣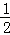 sinα,
sinα,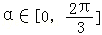 ,
,求导数可得S′=
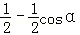 =
=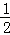 (1﹣cosα)>0,故S在区间
(1﹣cosα)>0,故S在区间 上单调递增,
上单调递增,S(0)=0,S(
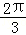 )=
)= ,
,故函数的值域为:[0,
 ]
]
练习册系列答案
相关题目
 的图象,只需要将函数
的图象,只需要将函数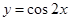 的图象( )
的图象( ) 个单位
个单位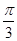 个单位
个单位 所对应的角,且
所对应的角,且 .
. 的值;
的值; ,求△ABC的面积的最大值。
,求△ABC的面积的最大值。 ,且
,且 ,则
,则 的值为: ( )
的值为: ( )



 的值是 ( )
的值是 ( )


 ,
, 是两个平行向量,则对于锐角
是两个平行向量,则对于锐角 ,
, 与
与 的大小关系是
的大小关系是


 的
的 的函数
的函数 关系式;
关系式;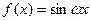 的图象向右平移
的图象向右平移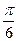 个单位得到
个单位得到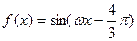 的图象,则|
的图象,则|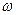 |的最小值为
|的最小值为  -2x)的单调增区间是( )
-2x)的单调增区间是( ) ,
, ](k
](k z)
z) ,
, ](k
](k ,
, ,
, ](k
](k