Question

【题目】设函数f（x）的定义域为R，f（x）= ，且对任意的x∈R都有f（x+1）=﹣ ，若在区间[﹣5，1]上函数g（x）=f（x）﹣mx+m恰有5个不同零点，则实数m的取值范围是（ ）
A.[﹣ ，﹣ ）
B.（﹣ ，﹣ ]
C.（﹣ ，0]
D.（﹣ ，﹣ ]

Answer 1

【答案】A
【解析】解：∵f（x+1）=﹣ ，∴f（x+2）=﹣ ， ∴f（x）=f（x+2），即f（x）的周期为2．
作出f（x）在[﹣5，1]上的函数图象如图所示：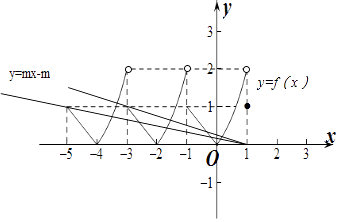

令g（x）=0得f（x）=mx﹣m，
则直线y=mx﹣m与f（x）在[﹣5，1]上有5个交点．
当直线y=mx﹣m过点（﹣3，1）时，直线y=mx﹣m与f（x）在[﹣5，1]上恰好有5个交点，
此时﹣3m﹣m=1，即m=﹣ ，
当直线y=mx﹣m过点（﹣5，1）时，直线y=mx﹣m与f（x）在[﹣5，1]上恰好有6个交点，
此时﹣5m﹣m=1，即m=﹣ ．
∴﹣ ≤m＜﹣ ．
故选A．