题目内容
f(x)是定义在(0,+∞)上的非负可导函数,且满足xf'(x)-f(x)<0,对任意正数a、b,若a<b,则必有
- A.af(b)<bf(a)
- B.af(b)>bf(a)
- C.af(a)>bf(b)
- D.af(a)<bf(b)
A
分析:先利用导数的除法运算,将已知不等式转化为函数y= 的导函数小于零,从而函数y=
的导函数小于零,从而函数y= 为(0,+∞)上为减函数,最后利用单调性比较自变量为a、b时函数值的大小即可变形得选项结果
为(0,+∞)上为减函数,最后利用单调性比较自变量为a、b时函数值的大小即可变形得选项结果
解答:∵xf'(x)-f(x)<0,∴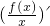 =
=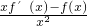 <0
<0
∴函数y= 为(0,+∞)上为减函数
为(0,+∞)上为减函数
∵0<a<b
∴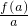 >
>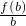
∴af(b)<bf(a)
故选 A
点评:本题主要考查了导数的四则运算,利用导数证明函数的单调性,利用函数的单调性比较函数值的大小,构造一个恰当的函数是解决本题的关键
分析:先利用导数的除法运算,将已知不等式转化为函数y=
 的导函数小于零,从而函数y=
的导函数小于零,从而函数y= 为(0,+∞)上为减函数,最后利用单调性比较自变量为a、b时函数值的大小即可变形得选项结果
为(0,+∞)上为减函数,最后利用单调性比较自变量为a、b时函数值的大小即可变形得选项结果解答:∵xf'(x)-f(x)<0,∴
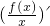 =
=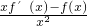 <0
<0∴函数y=
 为(0,+∞)上为减函数
为(0,+∞)上为减函数∵0<a<b
∴
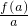 >
>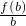
∴af(b)<bf(a)
故选 A
点评:本题主要考查了导数的四则运算,利用导数证明函数的单调性,利用函数的单调性比较函数值的大小,构造一个恰当的函数是解决本题的关键

练习册系列答案
相关题目