题目内容
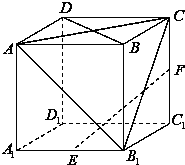 如图,在棱长为1的正方体ABCD-A1B1C1D1中,E,F分别是A1B1和CC1的中点.
如图,在棱长为1的正方体ABCD-A1B1C1D1中,E,F分别是A1B1和CC1的中点.(1)求异面直线BD与B1C所成的角;
(2)求证:EF∥平面ACB1.
分析:(1)连接B1D1,则DB∥D1B1,则∠D1B1C为异面直线BD与B1C所成的角,连接D1C,在△D1B1C中求解角;
(2)取B1D1的中点O,连接OE,OF,利用线面平行的判定定理,证明OE、OF分别与平面平行,从而得平面OEF∥平面AB1C,再由面面平行的性质得线面平行.
(2)取B1D1的中点O,连接OE,OF,利用线面平行的判定定理,证明OE、OF分别与平面平行,从而得平面OEF∥平面AB1C,再由面面平行的性质得线面平行.
解答: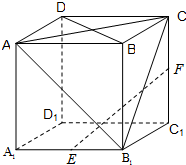 解:(1)如图,连接B1D1,则DB∥D1B1,
解:(1)如图,连接B1D1,则DB∥D1B1,
则∠D1B1C为异面直线BD与B1C所成的角,
连接D1C,在△D1B1C中,D1B1=B1C=CD1,
则∠D1B1C=60°,
因此异面直线BD与B1C所成的角为60°.
(2)取B1D1的中点O,连接OE,OF,A1C1,
∵O、F分别是B1C1,CC1的中点,∴OF∥B1C,
又B1C?平面AB1C,OF?平面AB1C,∴OF∥平面AB1C;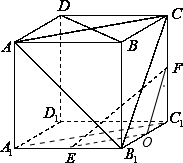
∵E为A1B1的中点,∴OE∥A1C1,又AC∥A1C1,∴OE∥AC,
又AC?平面AB1C,OE?平面AB1C,∴OE∥平面AB1C;
∵OE∩OF=O,∴平面OEF∥平面AB1C,EF?平面OEF,
∴EF∥平面AB1C.
 解:(1)如图,连接B1D1,则DB∥D1B1,
解:(1)如图,连接B1D1,则DB∥D1B1,则∠D1B1C为异面直线BD与B1C所成的角,
连接D1C,在△D1B1C中,D1B1=B1C=CD1,
则∠D1B1C=60°,
因此异面直线BD与B1C所成的角为60°.
(2)取B1D1的中点O,连接OE,OF,A1C1,
∵O、F分别是B1C1,CC1的中点,∴OF∥B1C,
又B1C?平面AB1C,OF?平面AB1C,∴OF∥平面AB1C;

∵E为A1B1的中点,∴OE∥A1C1,又AC∥A1C1,∴OE∥AC,
又AC?平面AB1C,OE?平面AB1C,∴OE∥平面AB1C;
∵OE∩OF=O,∴平面OEF∥平面AB1C,EF?平面OEF,
∴EF∥平面AB1C.
点评:本题考查了异面直线所成角的求法,考查了线面平行的判断,面面平行的判定及面面平行的性质,考查了学生的空间想象能力,逻辑推理能力.

练习册系列答案
 愉快的寒假南京出版社系列答案
愉快的寒假南京出版社系列答案
相关题目
 如图,在棱长都相等的正三棱柱ABC-A1B1C1中,D,E分别为AA1,B1C的中点.
如图,在棱长都相等的正三棱柱ABC-A1B1C1中,D,E分别为AA1,B1C的中点.
 如图,在棱长都相等的正三棱柱ABC-A1B1C1中,D,E分别为AA1,B1C的中点.
如图,在棱长都相等的正三棱柱ABC-A1B1C1中,D,E分别为AA1,B1C的中点.
