Question

（09年聊城期末）（12分）

       已知函数

   （1）若处取得极值？若能，求出实数的值，否则说明理由；

   （2）若函数内各有一个极值点，试求的取值范围。

Answer 1

解析：（1）由题意，

       …………2分

       若

       即

       函数为单调递增函数。

       这与该函数能在处取得极值矛盾，所以该函数不能在取到极值。……5分

   （2）因为函数在区间（-1，2），（2，3）内各有一个极值点。

       所以（-1，2），（2，3）内各有一个实根。

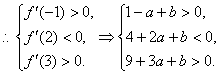       …………8分

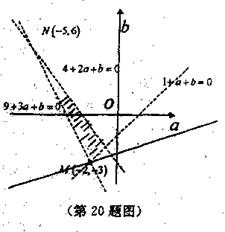
       画出不等式表示的区域如图所示，

将，

       当变化时，它表示斜率为轴上

的截距为的一组不行线。

       当直线向上移动时，截距增大，减小，

于是当目标函数过点N（-5，6），

       对应的最小；

当目标函数过点M（-2，-3），

对应的最大。

       所以的取值范围是…………12分