题目内容
（09年聊城期末理）（12分）
如图，矩形ABCD，
平面ABE，AE=EB=BC=2，F为CE是的点，且
平面ACE。
（1）求证：
平面BCE；
（2）求二面角B―AC―E的大小。
|
解析：（1）证明：
平面ABE，AD//BC。
平面ABE，则
…………2分
又
平面ACE，则
平面BCE。…………5分
|
（2）方法一：取AB的中点H，CD的中点N，则HN//AD
平面ABE，
平面ABE，
以HE所在直线为
轴，HB所在直线为
轴，
HN所在直线为z轴，
建立空间直角坐标系，
则，
平面BAC的一个法向量
…………8分
设平面EAC的一个法向量
，
由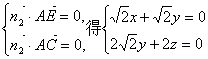
所以
令
…………10分
二面角B―AC―E的大小为60°…………12分
方法二：过Ｅ作
平面ABE，DA
平面ABCD，
平面ABCD
平面ABE，
平面ABCD。
|
平面EHM。
是
二面角B―AC―E的平面角。…………8分
在
∽
又
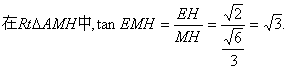
故二面角B―AC―E的大小为60°…………12分
练习册系列答案
相关题目
是等比数列；
的通项公式；
恒成立，求m的取值范围。
（点O为坐标原点），一条直线
与圆O相切，并与椭圆
交于不 同的两点A、B。
的表达式；
，求三角形OAB的面积。
的左、右焦点。若双曲线上存在点A，使
，则双曲线的离心率为 （ ）
B．
C．
D．
的充要条件是 （ ）
B．
C．
D．