题目内容
用数学归纳法证明:l3+23+33+…+n3=| n2+(n+1)2 | 4 |
分析:应用数学归纳法证明问题,①验证n=1时命题成立;②假设n=k时,命题成立,从假设出发,经过推理论证,证明n=k+1时也成立,从而证明命题正确.
解答:证明:①当n=1时,左边=1,右边=1,∴n=1时,等式成立.
②假设n=k时,等式成立,即13+23+33++k3=
k2(k+1)2
13+23+33++k3+(k+1)3
=
k2(k+1)2+(k+3)3=
(k+1)2[k2+4(k+1)]=
(k+1)2[(k+1)+1]2
∴n=k+1时,等式成立.
综合①、②原等式获证.
②假设n=k时,等式成立,即13+23+33++k3=
| 1 |
| 4 |
13+23+33++k3+(k+1)3
=
| 1 |
| 4 |
| 1 |
| 4 |
| 1 |
| 4 |
∴n=k+1时,等式成立.
综合①、②原等式获证.
点评:考查数学归纳法证明有关正整数命题的方法步骤,特别是②是关键,是核心,也是数学归纳法证明命题的难点所在,属基础题.

练习册系列答案
相关题目
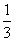 x3-x2(x∈R),
x3-x2(x∈R), n∈N*,ex-1>
n∈N*,ex-1>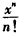 。
。 +
+ +L+
+L+ (n∈N*),用数学归纳法证明f(2n)>
(n∈N*),用数学归纳法证明f(2n)>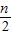 时,f(2k+1)-f(2k)等于 .
时,f(2k+1)-f(2k)等于 .