题目内容
已知m∈R,设p:复数z1=(m-1)+(m+3)i (i是虚数单位)在复平面内对应的点在第二象限,q:复数z2=1+(m-2)i的模不超过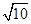 .
.
(1)当p为真命题时,求m的取值范围;
(2)若命题“p且q”为假命题,“p或q”为真命题,求m的取值范围.
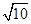 .
.(1)当p为真命题时,求m的取值范围;
(2)若命题“p且q”为假命题,“p或q”为真命题,求m的取值范围.
(1)(-3,1) (2)(-3,-1)∪[1,5]
试题分析:(1)复数
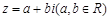 对应的点为
对应的点为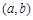 ,所以有
,所以有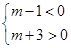 ,从而可解得m的取值范围为(-3,1),(2)因为命题“p且q”一假就假,所以p,q中至少有一个为假;因为命题“p或q”一真就真,所以p,q中至少有一个为真;综合得p,q中一真一假.若q为真,则q为假;或若q为假,则q为真.先求命题为真时参数范围,再根据集合的补集求命题为假时参数范围.
,从而可解得m的取值范围为(-3,1),(2)因为命题“p且q”一假就假,所以p,q中至少有一个为假;因为命题“p或q”一真就真,所以p,q中至少有一个为真;综合得p,q中一真一假.若q为真,则q为假;或若q为假,则q为真.先求命题为真时参数范围,再根据集合的补集求命题为假时参数范围.试题解析:解(1)因为复数z1=(m-1)+(m+3)i在复平面内对应的点在第二象限,
所以
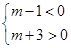
解得-3<m<1,即m的取值范围为(-3,1). 3分
(2)由q为真命题,即复数z2=1+(m-2)i的模不超过
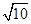 ,
,所以
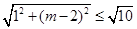 ,解得-1≤m≤5. 5分
,解得-1≤m≤5. 5分由命题“p且q”为假命题,“p或q”为真命题
得
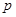 真
真 假或
假或 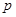 假
假 真,所以
真,所以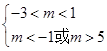 或
或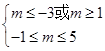
即-3<m<-1或1≤m≤5.
所以m的取值范围为(-3,-1)∪[1,5]. 8分

练习册系列答案
相关题目
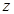 为复数,且
为复数,且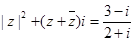 (
(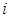 为虚数单位),求
为虚数单位),求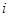 为虚数单位,在复平面内复数
为虚数单位,在复平面内复数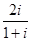 对应点的坐标为__________.
对应点的坐标为__________.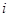 是虚数单位,则复数
是虚数单位,则复数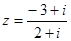 的共轭复数是_____________
的共轭复数是_____________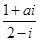 为纯虚数,则实数a为( ).
为纯虚数,则实数a为( ).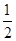
 满足
满足 ,则
,则 ( )
( )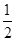



 (
(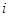 为虚数单位),则
为虚数单位),则 ( )
( )



 的共轭复数为 ( ).
的共轭复数为 ( ). i
i