题目内容

函数f（x）=ax3+bx在x=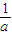处有极值，则ab的值为（ ）
A．3
B．-3
C．0
D．1
【答案】分析：先对函数进行求导，然后根据f'（）=0，可求出ab的值．
解答：解：∵f（x）=ax3+bx，
∴f′（x）=3ax2+b．
由函数f（x）=ax3+bx在x=处有极值，
则f′（）=3a（）2+b=0，⇒ab=-3．
故选B．
点评：此题是个中档题．本题主要考查极值与其导函数之间的关系．导数是高等数学下放到高中的内容，是高考的热点问题，每年必考，要给予充分重视．
练习册系列答案
相关题目
有下列命题：
①若f（x）存在导函数，则f′（2x）=[f（2x）]′．
②若函数h（x）=cos4x-sin4x，则h′(
π12
)=1；
③若函数g（x）=（x-1）（x-2）…（x-2009）（x-2010），则g′（2010）=2009!．
④若三次函数f（x）=ax3+bx2+cx+d，则“a+b+c=0”是“f（x）有极值点”的充要条件．
其中真命题的序号是
 
．
18、已知函数f（x）=ax3-6ax2+b（x∈[-1，2]）的最大值为3，最小值为-29，求a、b的值．
对于三次函数f（x）=ax3+bx2+cx+d（a≠0）．
定义：（1）设f″（x）是函数y=f（x）的导数y=f′（x）的导数，若方程f″（x）=0有实数解x0，则称点（x0，f（x0））为函数y=f（x）的“拐点”；
定义：（2）设x0为常数，若定义在R上的函数y=f（x）对于定义域内的一切实数x，都有f（x0+x）+f（x0-x）=2f（x0）成立，则函数y=f（x）的图象关于点（x0，f（x0））对称．
己知f（x）=x3-3x2+2x+2，请回答下列问题：
（1）求函数f（x）的“拐点”A的坐标
 
；
（2）检验函数f（x）的图象是否关于“拐点”A对称，对于任意的三次函数写出一个有关“拐点”的结论
 
．
若函数f（x）=ax3-2x2+a2x在x=1处有极小值，则实数a等于
1
1
．
已知下表为函数f（x）=ax3+cx+d部分自变量取值及其对应函数值，为了便于研究，相关函数值取非整数值时，取值精确到0.01．
x -0.61 -0.59 -0.56 -0.35 0 0.26 0.42 1.57 3.27
y 0.07 0.02 -0.03 -0.22 0 0.21 0.20 -10.04 -101.63
根据表中数据，研究该函数的一些性质：
（1）判断f（x）的奇偶性，并证明；
（2）判断f（x）在[0.55，0.6]上是否存在零点，并说明理由．

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网