题目内容
已知函数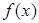 是定义在
是定义在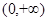 上的单调函数,且对任意的正数
上的单调函数,且对任意的正数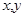 都有
都有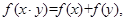 若数列
若数列 的前
的前 项和为
项和为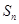 ,且满足
,且满足 则
则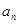 为( )
为( )
A.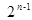 | B.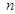 | C.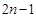 | D.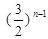 |
D
解析试题分析:因为对任意的正数x,y都有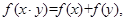
又 ,所以f(sn+2)=f(3)+f(an)=f(3•an),
,所以f(sn+2)=f(3)+f(an)=f(3•an),
因为函数f(x)是定义在(0,+∞)上的单调函数,
所以sn+2=3an………………………………①
当n=1时,s1+2=a1+2=3a1,解得an=1;
当n≥2时,sn-1+2=3an-1………………②
①-②得:an=3an-3an-1
即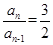 ,所以数列{an}是一个以1为首项,以
,所以数列{an}是一个以1为首项,以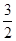 为公比的等比数列,所以
为公比的等比数列,所以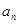 =
=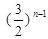 。
。
考点:数列与函数的综合应用;数列通项公式的求法。
点评:本题以抽象函数为载体考查了等比数列通项公式的求法,其中根据已知得到f(sn+2)=f(3)+f(an)=f(3•an)是解答的关键。

练习册系列答案
相关题目
定义在R上的函数 满足:
满足: 成立,且
成立,且 上单调递增,设
上单调递增,设 ,则a、b、c的大小关系是 ( )
,则a、b、c的大小关系是 ( )
A. | B. | C. | D. |
函数 的零点所在的区间为 ( )
的零点所在的区间为 ( )
A.(1, ) ) | B.( ,2) ,2) | C.(2,e) | D.(e,+∞) |
函数f(x)= cos2x在区间[-3,3]上的零点的个数为( )
cos2x在区间[-3,3]上的零点的个数为( )
| A.3 | B.4 | C.5 | D.6 |
已知函数 是R上的偶函数,当x
是R上的偶函数,当x 0时
0时 ,则
,则 的解集是
的解集是
| A.(-1,0) | B.(0,1) |
| C.(-1,1) | D. |
设偶函数 在
在 上是增函数,则
上是增函数,则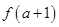 与
与 的
的
大小关系是( )
A. | B. |
C. | D.不能确定 |
关于狄利克雷函数 的叙述错误的是 ( )
的叙述错误的是 ( )
A. 的值域是 的值域是 | B. 是偶函数 是偶函数 |
C. 是奇函数 是奇函数 | D. 的定义域是 的定义域是 |
 ]的函数
]的函数 图像的两个端点为A、B,M(x,y)是
图像的两个端点为A、B,M(x,y)是 图象上任意一点,其中
图象上任意一点,其中 .已知向量
.已知向量 ,若不等式
,若不等式 恒成立, 则称函数
恒成立, 则称函数 在[
在[ 在[1,2]上“k阶线性近似”,则实数k的取值范围为( )
在[1,2]上“k阶线性近似”,则实数k的取值范围为( )
 D.
D.
 的图像大致是
的图像大致是