题目内容
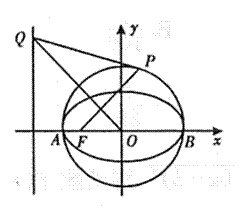
已知圆![]() 轴于A,B两点,曲线C是以AB为长轴,离心率为
轴于A,B两点,曲线C是以AB为长轴,离心率为![]() 的椭圆,其左焦点为F.若P是圆O上一点,连结PF,过原点作直线PF的垂线交直线
的椭圆,其左焦点为F.若P是圆O上一点,连结PF,过原点作直线PF的垂线交直线![]() 于点Q.
于点Q.
 (1)求椭圆C的标准方程;w.w.w.k.s.5.u.c.o.m
(1)求椭圆C的标准方程;w.w.w.k.s.5.u.c.o.m ![]()
(2)若点P的坐标为(1,1),求证:直线PQ圆O相切;
(3)试探究:当点P在圆O上运动时(不与A、B重合),直线PQ与圆O是否保持相切的位置关系?若是,请证明;若不是,请说明理由(一、二、五中必做,其它学校选做)。.
解析:(1)因为![]() (2分)
(2分)
则b=1,即椭圆C的标准方程为![]() (3分)
(3分)
(2)因为P(1,1),所以![]()
所以![]() ,所以直线OQ的方程为y= ―2x. (4分)
,所以直线OQ的方程为y= ―2x. (4分)
又Q在直线![]() 上,所以点Q(―2,4) (5分)w.w.w.k.s.5.u.c.o.m
上,所以点Q(―2,4) (5分)w.w.w.k.s.5.u.c.o.m ![]()
![]()
![]() 即QP⊥OQ,
即QP⊥OQ,
故直线PQ与圆O相切, (6分)
(3)当点P在圆O上运动时,直线PQ与圆P保持相切的位置关系. (7分)
设![]() ,则
,则![]()
所以直线OQ的方程为![]() 所以点Q
所以点Q![]() (10分)
(10分)
所以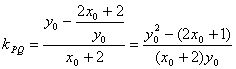 w.w.w.k.s.5.u.c.o.m
w.w.w.k.s.5.u.c.o.m ![]()
![]()
所以![]() ,即OP⊥PQ(P不与A、B重合),
,即OP⊥PQ(P不与A、B重合),

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
已知椭圆C1:
+
=1(a>b>0)与双曲线C2:x2-
=1有公共的焦点,C2的一条渐近线与以C1的长轴为直径的圆相交于A,B两点.若C1恰好将线段AB三等分,则( )
| x2 |
| a2 |
| y2 |
| b2 |
| y2 |
| 4 |
A、a2=
| ||
| B、a2=3 | ||
C、b2=
| ||
| D、b2=2 |
 如图,已知圆O:x2+y2=2交x轴于A,B两点,点P(-1,1)为圆O上一点.曲线C是以AB为长轴,离心率为
如图,已知圆O:x2+y2=2交x轴于A,B两点,点P(-1,1)为圆O上一点.曲线C是以AB为长轴,离心率为 已知:如图,圆O:x2+y2=2交x轴于A,B两点,曲线C是以AB为长轴,离心率为
已知:如图,圆O:x2+y2=2交x轴于A,B两点,曲线C是以AB为长轴,离心率为