题目内容
18.已知函数f(x)=$\left\{\begin{array}{l}{x+2,x≤-2}\\{{x}^{2},-2<x<2}\\{2x,x≥2}\end{array}\right.$,(1)求f(-3),f[f(-3)].
(2)若f(a)=8,求a的值.
分析 (1)判断x的值所在的范围,代入分段函数求解即可;
(2)由f(a)=8可得$\left\{{\begin{array}{l}{a≤-2}\\{a+2=8}\end{array}}\right.$或$\left\{{\begin{array}{l}{-2<a<2}\\{{a^2}=8}\end{array}}\right.$或$\left\{{\begin{array}{l}{a≥2}\\{2a=8}\end{array}}\right.$,从而解得.
解答 解:(1)f(-3)=-3+2=-1,
f[f(-3)]=f(-1)=(-1)2=1;
(2)∵f(a)=8,
∴$\left\{{\begin{array}{l}{a≤-2}\\{a+2=8}\end{array}}\right.$或$\left\{{\begin{array}{l}{-2<a<2}\\{{a^2}=8}\end{array}}\right.$或$\left\{{\begin{array}{l}{a≥2}\\{2a=8}\end{array}}\right.$,
解得,a=4.
点评 本题考查了分段函数的一般解法及分类讨论的思想应用.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
9.一个金鱼缸,现已注满水.有大、中、小三个假山,第一次把小假山沉入水中,第二次把小假山取出,把中假山沉入水中,第三次把中假山取出,把小假山和大假山一起沉入水中,现知道每次溢出水量的情况是:第一次是第二次的$\frac{1}{3}$.第三次是第二次的2倍,问三个假山体积之比( )
| A. | 1:3:5 | B. | 1:4:9 | C. | 3:6:7 | D. | 6:7:8 |
6.等差数列{an}的前n项和为Sn,若当首项a1和公差d变化时,a3+a10+a11是一个定值,则下列选项中为定值的是( )
| A. | S17 | B. | S16 | C. | S15 | D. | S14 |
3.函数f(x)=log2(4-x2)定义域为( )
| A. | [-2,2] | B. | (-2,2) | C. | (-∞,2)∪(2,+∞) | D. | (-∞,2]∪[2,+∞) |
7.下列命题中,正确命题的序号为( )
| A. | 命题p:?x∈R,使得x2-1≥0,命题q:?x∈R,使得x2-x-1≥0,则命题p∨¬q是假命题 | |
| B. | 非零向量$\overrightarrow{a}$,$\overrightarrow{b}$,“$\overrightarrow{a}$•$\overrightarrow{b}$>0”是“$\overrightarrow{a}$与$\overrightarrow{b}$夹角是锐角”的充要条件 | |
| C. | “两直线2x-my-1=0与x+my-1=0垂直”是“$m=±\sqrt{2}$”的充要条件 | |
| D. | “a=1”是“函数f(x)=x2+|x+a-1|(x∈R)为偶函数”的充分不必要条件 |
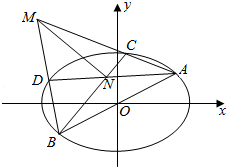 如图,在平面直角坐标系xoy中,椭圆E:$\frac{x^2}{a^2}$+$\frac{y^2}{b^2}$=1(a>b>0)的离心率为$\frac{{\sqrt{2}}}{2}$,直线l:y=$\frac{1}{2}$x与椭圆E相交于A,B两点,AB=$4\sqrt{5}$,C,D是椭圆E上异于A,B两点,且直线AC,BD相交于点M,直线AD,BC相交于点N.
如图,在平面直角坐标系xoy中,椭圆E:$\frac{x^2}{a^2}$+$\frac{y^2}{b^2}$=1(a>b>0)的离心率为$\frac{{\sqrt{2}}}{2}$,直线l:y=$\frac{1}{2}$x与椭圆E相交于A,B两点,AB=$4\sqrt{5}$,C,D是椭圆E上异于A,B两点,且直线AC,BD相交于点M,直线AD,BC相交于点N.