题目内容
(本小题满分 分)已知函数
分)已知函数 (
( ,
, 是不同时为零的常数).
是不同时为零的常数).
(1)当 时,若不等式
时,若不等式 对任意
对任意 恒成立,求实数
恒成立,求实数 的取值范围;
的取值范围;
(2)求证:函数 在
在 内至少存在一个零点.
内至少存在一个零点.
【答案】
(1)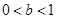 (2)
(2)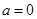 时易证结论;
时易证结论;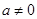 时,利用函数的零点存在定理可以证明结论成立.
时,利用函数的零点存在定理可以证明结论成立.
【解析】
试题分析:(1)当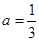 时,
时,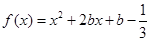 ,
,
由不等式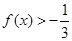 即
即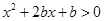 对任意
对任意 恒成立,
恒成立,
得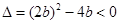 ,解得
,解得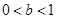 . ……5分
. ……5分
(2)证明:当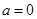 时,因为
时,因为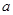 ,
,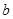 不同时为零,所以
不同时为零,所以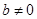 ,
,
所以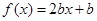 的零点为
的零点为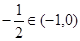 , ……6分
, ……6分
当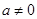 时,二次函数
时,二次函数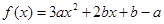 的对称轴方程为
的对称轴方程为 , ……7分
, ……7分
①若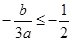 即
即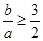 时,
时,
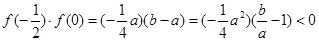 ,
,
∴函数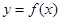 在
在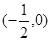 内至少存在一个零点. ……10分
内至少存在一个零点. ……10分
②若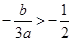 即
即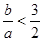 时,
时,
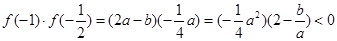 ,
,
∴函数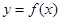 在
在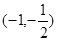 内至少存在一个零点. ……13分
内至少存在一个零点. ……13分
综上得:函数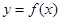 在
在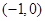 内至少存在一个零点. ……14分
内至少存在一个零点. ……14分
考点:本小题主要考查二次函数恒成立问题和函数零点存在定理的应用,考查学生的转化能力和运算求解能力以及分类讨论思想的应用.
点评:恒成立问题,一般转化为最值问题解决,而函数的零点存在定理能确定一定存在零点,但是确定不了存在几个零点.

练习册系列答案
相关题目
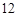 分)已知函数
分)已知函数 ,
,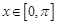 ,求该函数的单调递增区间。
,求该函数的单调递增区间。 分)
分) 的左、 右顶点分别为
的左、 右顶点分别为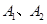 ,动直线
,动直线 与圆
与圆 相切,且与双曲线左、右两支的交点分别为
相切,且与双曲线左、右两支的交点分别为 .
.
 的取值范围,并求
的取值范围,并求 的最小值;
的最小值; 的斜率为
的斜率为 ,直线
,直线 的斜率为
的斜率为 ,那么,
,那么, 是定值吗?并证明
是定值吗?并证明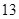 分)
分)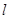 与抛物线
与抛物线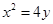 相切于点
相切于点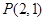 ,且与
,且与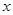 轴交于点
轴交于点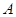 ,定点
,定点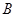 的坐标为
的坐标为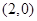 .
.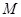 满足
满足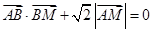 ,求点
,求点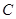 ;
;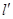 (斜率不等于零)与(I)中的轨迹
(斜率不等于零)与(I)中的轨迹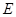 、
、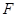 (
(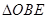 与
与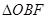 面积之比的取值范围.
面积之比的取值范围. 分)
分)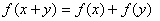 对于任何实数
对于任何实数 ,y都成立,
,y都成立, ;
; 的值;
的值; 为奇函数。
为奇函数。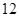 分)
分)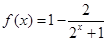 ,
,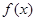 的值域。
的值域。