题目内容
如图,已知ABC-A1B1C1是正三棱柱,D是AC中点,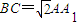 .
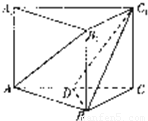
.(I)证明AB1∥平面DBC1
(II)求异面直线AB1与BC1所成的角
(III)求以BC1为棱,DBC1与CBC1为面的二面角的度数.
【答案】分析:(I)要证明线面平行,需要在面上找一条和已知直线平行的直线,根据四边形B1BCC1是矩形.连接B1C交BC1于E,则B1E=EC.连接DE,在△AB1C中,AD=DC,得到DE∥AB1,这样题目得证.
(II)以DB为x轴,DC为y轴,DD1为z轴建立空间直角坐标系,写出要用的点的坐标,构造两个向量的方向向量,方向向量所成的角的余弦值的绝对值就是要求的角的余弦值,本题比较特殊是一个直角.
(III)要求两个平面所成的角,需要先写出两个平面的法向量,其中这两个平面有一个法向量是已知的,另一个需要设出来,再根据法向量与平面上的向量数量积等于0,写出一个法向量,根据向量所成的角得到结果.
解答:解: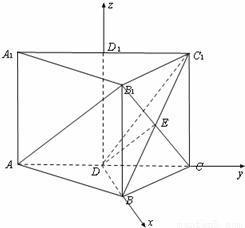 (Ⅰ)证明:∵A1B1C1-ABC是正三棱柱,
(Ⅰ)证明:∵A1B1C1-ABC是正三棱柱,
∴四边形B1BCC1是矩形.
连接B1C交BC1于E,则B1E=EC.
连接DE,在△AB1C中,∵AD=DC,∴DE∥AB1,
又AB1?平面DBC1,DE?平面DBC1,
∴AB1∥平面DBC1.
(Ⅱ)设D1是A1C1的中点,则DD1⊥平面ABC.
所以,以DB为x轴,DC为y轴,DD1为z轴(如图)建立空间直角坐标系.
设AB=2,则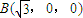 ,C(0,1,0),A(0,-1,0),
,C(0,1,0),A(0,-1,0),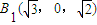 ,
,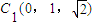 .
.
∴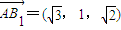 ,
, ,
,
∵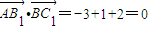 ,∴
,∴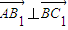 ,
,
即,AB1与BC1所成的角为90°.
(Ⅲ)∵BC的中点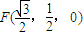 ,
,
∴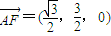 ,
,
∴可取平面CBC1的法向量为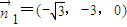 .
.
设平面BC1D的法向量为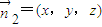 ,
,
则 ⇒
⇒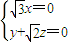
∴可取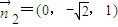 .
.
∵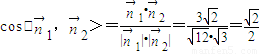 ,
,
∴面DBC1与面CBC1所成的二面角为45°.
点评:本题考查利用空间向量求解两个平面之间的夹角和异面直线所成的角,本题解题的关键是建立坐标系,本题理论推导的问题转化成数字的运算问题,本题是一个中档题目.
(II)以DB为x轴,DC为y轴,DD1为z轴建立空间直角坐标系,写出要用的点的坐标,构造两个向量的方向向量,方向向量所成的角的余弦值的绝对值就是要求的角的余弦值,本题比较特殊是一个直角.
(III)要求两个平面所成的角,需要先写出两个平面的法向量,其中这两个平面有一个法向量是已知的,另一个需要设出来,再根据法向量与平面上的向量数量积等于0,写出一个法向量,根据向量所成的角得到结果.
解答:解:
 (Ⅰ)证明:∵A1B1C1-ABC是正三棱柱,
(Ⅰ)证明:∵A1B1C1-ABC是正三棱柱,∴四边形B1BCC1是矩形.
连接B1C交BC1于E,则B1E=EC.
连接DE,在△AB1C中,∵AD=DC,∴DE∥AB1,
又AB1?平面DBC1,DE?平面DBC1,
∴AB1∥平面DBC1.
(Ⅱ)设D1是A1C1的中点,则DD1⊥平面ABC.
所以,以DB为x轴,DC为y轴,DD1为z轴(如图)建立空间直角坐标系.
设AB=2,则
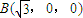 ,C(0,1,0),A(0,-1,0),
,C(0,1,0),A(0,-1,0),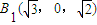 ,
,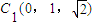 .
.∴
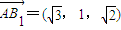 ,
, ,
,∵
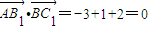 ,∴
,∴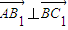 ,
,即,AB1与BC1所成的角为90°.
(Ⅲ)∵BC的中点
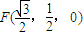 ,
,∴
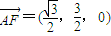 ,
,∴可取平面CBC1的法向量为
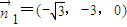 .
.设平面BC1D的法向量为
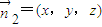 ,
,则
 ⇒
⇒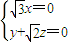
∴可取
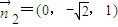 .
.∵
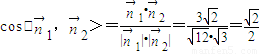 ,
,∴面DBC1与面CBC1所成的二面角为45°.
点评:本题考查利用空间向量求解两个平面之间的夹角和异面直线所成的角,本题解题的关键是建立坐标系,本题理论推导的问题转化成数字的运算问题,本题是一个中档题目.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
 如图,已知△ABC的顶点为A(2,4),B(0,-2),C(-2,3),求:
如图,已知△ABC的顶点为A(2,4),B(0,-2),C(-2,3),求: 如图,已知△ABC是正三角形,EA、CD都垂直于平面ABC,且EA=AB=2a,DC=a,F是BE的中点,求证:
如图,已知△ABC是正三角形,EA、CD都垂直于平面ABC,且EA=AB=2a,DC=a,F是BE的中点,求证: 如图,已知两点A(-
如图,已知两点A(-
 如图,已知△ABC内接于圆O,AB是圆O的直径,四边形DCBE为平行四边形,DC⊥平面ABC,AB=2,
如图,已知△ABC内接于圆O,AB是圆O的直径,四边形DCBE为平行四边形,DC⊥平面ABC,AB=2,