题目内容
已知函数 (
( ),其中
),其中 .
.
(1)当 时,讨论函数
时,讨论函数 的单调性;
的单调性;
(2)若函数 仅在
仅在 处有极值,求
处有极值,求 的取值范围;
的取值范围;
(3)若对于任意的 ,不等式
,不等式 在
在 上恒成立,求
上恒成立,求 的取值范围.
的取值范围.
【答案】
(1) .
.
当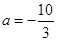 时,
时,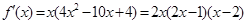 .令
.令 ,解得
,解得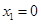 ,
,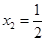 ,
,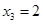 . 当
. 当 变化时,
变化时,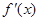 ,
, 的变化情况如下表:
的变化情况如下表:
|
|
|
0 |
|
|
|
2 |
|
|
|
- |
0 |
+ |
0 |
- |
0 |
+ |
|
|
↘ |
极小值 |
↗ |
极大值 |
↘ |
极小值 |
↗ |
所以 在
在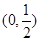 ,
, 内是增函数,在
内是增函数,在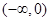 ,
,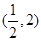 内是减函数.
内是减函数.
(2) ,显然
,显然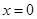 不是方程
不是方程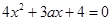 的根.
的根.
为使 仅在
仅在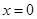 处有极值,必须
处有极值,必须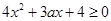 恒成立,即有
恒成立,即有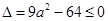 .
.
解此不等式,得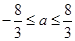 .这时,
.这时, 是唯一极值.
是唯一极值.
因此满足条件的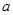 的取值范围是
的取值范围是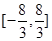 .
.
(3)由条件 及(II)可知,
及(II)可知, .
.
从而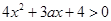 恒成立.
恒成立.
当 时,
时,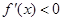 ;当
;当 时,
时, .
.
因此函数 在
在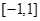 上的最大值是
上的最大值是 与
与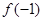 两者中的较大者.
两者中的较大者.
为使对任意的 ,不等式
,不等式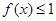 在
在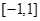 上恒成立,当且仅当
上恒成立,当且仅当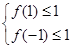 ,
,
即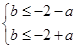 ,在
,在 上恒成立.所以
上恒成立.所以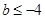 .
.
因此满足条件的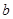 的取值范围是
的取值范围是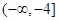 .
.
【解析】略

练习册系列答案
 王后雄学案教材完全解读系列答案
王后雄学案教材完全解读系列答案
相关题目
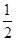
 (
(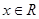 ),其中
),其中 .
. ,
, 时,求函数
时,求函数 的单调区间和极值;
的单调区间和极值; 处有极值,求实数
处有极值,求实数 的取值范围;
的取值范围; ,不等式
,不等式 在
在 上恒成立,求实数
上恒成立,求实数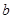 的取值范围.
的取值范围.  ,其中n∈N,则f(8)等于
,其中n∈N,则f(8)等于
 (
( ),其中
),其中 .
. 仅在
仅在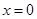 处有极值,求
处有极值,求 的取值范围;
的取值范围; ,不等式
,不等式 在
在 上恒成立,求
上恒成立,求 的取值范围.
的取值范围.