题目内容
当a为任意实数时,直线(2a+3)x+y-4a+2=0恒过定点P,则过点P的抛物线的标准方程是( )A.x2=32y或
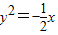
B.x2=-32y或
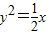
C.y2=32x或
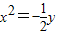
D.y2=-32x或
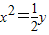
【答案】分析:将直线方程转化为(2x-4)a+3x+y+2=0求出定点坐标,然后分别设焦点在x轴和在y轴两种情况的抛物线的方程,将定点代入即可得到答案.
解答:解:将直线方程化为(2x-4)a+3x+y+2=0,可得定点P(2,-8),
①设抛物线y2=ax代入点P可求得a=32,故y2=32x
②设抛物线x2=by代入点P可求得b=- ,故
,故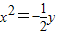
故选C.
点评:本题主要考查抛物线的标准方程.属基础题.
解答:解:将直线方程化为(2x-4)a+3x+y+2=0,可得定点P(2,-8),
①设抛物线y2=ax代入点P可求得a=32,故y2=32x
②设抛物线x2=by代入点P可求得b=-
 ,故
,故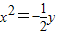
故选C.
点评:本题主要考查抛物线的标准方程.属基础题.

练习册系列答案
 芝麻开花课程新体验系列答案
芝麻开花课程新体验系列答案
相关题目
当a为任意实数时,直线(a-1)x-y+2a+1=0恒过定点P,则过点P的抛物线的标准方程是( )
A、y2=-
| ||||
B、y2=
| ||||
C、y2=
| ||||
D、y2=-
|
当a为任意实数时,直线(2a+3)x+y-4a+2=0恒过定点P,则过点P的抛物线的标准方程是( )
A、x2=32y或y2=-
| ||
B、x2=-32y或y2=
| ||
C、y2=32x或x2=-
| ||
D、y2=-32x或x2=
|