题目内容
【题目】已知函数f（x）=x2+4x+a﹣5，g（x）=m4x﹣1﹣2m+7．
（1）若函数f（x）在区间[﹣1，1]上存在零点，求实数a的取值范围；
（2）当a=0时，若对任意的x1∈[1，2]，总存在x2∈[1，2]，使f（x1）=g（x2）成立，求实数m的取值范围；
（3）若y=f（x）（x∈[t，2]）的置于为区间D，是否存在常数t，使区间D的长度为6﹣4t？若存在，求出t的值；若不存在，请说明理由． （注：区间[p，q]的长度q﹣p）
【答案】
（1）解：由题意得：f（x）的对称轴是x=﹣2，
故f（x）在区间[﹣1，1]递增，
∵函数在区间[﹣1，1]存在零点，
故有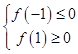 
，即 
，解得：0≤a≤8，
故所求实数a的范围是[0，8]
（2）解：若对任意的x1∈[1，2]，总存在x2∈[1，2]，使f（x1）=g（x2）成立，
只需函数y=f（x）的值域是函数y=g（x）的值域的子集，
a=0时，f（x）=x2+4x﹣5，x∈[1，2]的值域是[0，7]，
下面求g（x），x∈[1，2]的值域，
令t=4x﹣1，则t∈[1，4]，y=mt﹣2m+7，
①m=0时，g（x）=7是常数，不合题意，舍去；
②m＞0时，g（x）的值域是[7﹣m，2m+7]，
要使[0，7][7﹣m，2m+7]，
只需 
，解得：m≥7；
③m＜0时，g（x）的值域是[2m+7，7﹣m]，
要使[0，7][2m+7，7﹣m]，
只需 
，解得：m≤﹣ 
，
综上，m的范围是（﹣∞，﹣ ]∪[7，+∞）
（3）解：由题意得 
，解得：t＜ 
，
①t≤﹣6时，在区间[t，2]上，f（t）最大，f（﹣2）最小，
∴f（t）﹣f（﹣2）=t2+4t+4=6﹣4t，
即t2+8t﹣2=0，解得：t=﹣4﹣3 
或t=﹣4+3 （舍去）；
②﹣6＜t≤﹣2时，在区间[t，2]上，f（2）最大，f（﹣2）最小，
∴f（2）﹣f（﹣2）=16=6﹣4t，解得：t=﹣ 
；
③﹣2＜t＜ 时，在区间[t，2]上，f（2）最大，f（t）最小，
∴f（2）﹣f（t）=﹣t2﹣4t+12=6﹣4t，
即t2=6，解得：t= 
或t=﹣ ，
故此时不存在常数t满足题意，
综上，存在常数t满足题意，
t=﹣4﹣3 或t=﹣
【解析】（1）求出函数的对称轴，得到函数的单调性，解关于a的不等式组，解出即可；（2）只需函数y=f（x）的值域是函数y=g（x）的值域的子集，通过讨论m=0，m＞0，m＜0的情况，得到函数的单调性，从而确定m的范围即可；（3）通过讨论t的范围，结合函数的单调性以及f（2），f（﹣2）的值，得到关于t的方程，解出即可．
【考点精析】关于本题考查的利用导数研究函数的单调性和函数的最大(小)值与导数，需要了解一般的,函数的单调性与其导数的正负有如下关系： 在某个区间
内，(1)如果
，那么函数
在这个区间单调递增；(2)如果
，那么函数
在这个区间单调递减；求函数在
上的最大值与最小值的步骤：（1）求函数在内的极值；（2）将函数的各极值与端点处的函数值
，
比较，其中最大的是一个最大值，最小的是最小值才能得出正确答案．
【题目】某同学用“五点法”画函数f（x）=Asin（ωx+φ）（ω＞0，|φ|＜ 
）在某一个周期内的图象时，列表并填入了部分数据，如表：
ωx+φ | 0 |
| π |
| 2π |
x | | | |||
f（x） | 0 | 3 | 0 | ﹣3 | 0 |
（1）请将表中数据补充完整，并直接写出函数f（x）的解析式；
（2）若将函数f（x）的图象上所有点的横坐标变为原来的2倍，纵坐标不变，得到函数g（x）的图象，求当x∈[﹣ 
， ]时，函数g（x）的值域；
（3）若将y=f（x）图象上所有点向左平移θ（θ＞0）个单位长度，得到y=h（x）的图象，若=h（x）图象的一个对称中心为（ 
），求θ的最小值．
