题目内容
21、已知定义域在R上的函数f(x)满足f(x+y)=f(x)+f(y),且当x>0时,f(x)>0,
(1)求f(0).
(2)判断函数的奇偶性,并证明之.
(3)解不等式f(a2-4)+f(2a+1)<0.
(1)求f(0).
(2)判断函数的奇偶性,并证明之.
(3)解不等式f(a2-4)+f(2a+1)<0.
分析:解决此类问题的关键是利用好条件中的函数性质等式.(1)利用赋值法求f(0)的值;(2)利用赋值法及定义证明函数的奇偶性;(3)利用函数的单调性解不等式.
解答:解:(1)取x=y=0则f(0)=2f(0)∴f(0)=0
(2)f(x)是奇函数.其证明如下:
对任意x∈R,取y=-x则f[x+(-x)]=f(x)+f(-x)=f(0)=0即f(-x)=-f(x)
∴f(x)是R上的奇函数
(3)任意取x1,x2∈R,x1<x2,则x2=x1+△x(其中△x>0)
∴f(x2)=f(x1+△x)=f(x1)+f(△x)
∴f(x2)-f(x1)=f(△x)>0即f(x2)>f(x1)
∴f(x)是R上的增函数
又∵f(a2-4)+f(2a+1)<0
∴f(2a+1)<-f(a2-4)=f(4-a2)
∴2a+1<4-a2即a2+2a-3<0
∴-3<a<1
(2)f(x)是奇函数.其证明如下:
对任意x∈R,取y=-x则f[x+(-x)]=f(x)+f(-x)=f(0)=0即f(-x)=-f(x)
∴f(x)是R上的奇函数
(3)任意取x1,x2∈R,x1<x2,则x2=x1+△x(其中△x>0)
∴f(x2)=f(x1+△x)=f(x1)+f(△x)
∴f(x2)-f(x1)=f(△x)>0即f(x2)>f(x1)
∴f(x)是R上的增函数
又∵f(a2-4)+f(2a+1)<0
∴f(2a+1)<-f(a2-4)=f(4-a2)
∴2a+1<4-a2即a2+2a-3<0
∴-3<a<1
点评:抽象函数求值问题的方法就是赋值.判断抽象函数的奇偶性和单调性通常应用定义法.抽象函数解不等式应利用函数的单调性及奇偶性来解决.

练习册系列答案
 小学学习好帮手系列答案
小学学习好帮手系列答案 小学同步三练核心密卷系列答案
小学同步三练核心密卷系列答案
相关题目
已知下表为定义域为R的函数f(x)=ax3+cx+d若干自变量取值及其对应函数值,为便于研究,相关函数值非整数值时,取值精确到0.01.
根据表中数据解答下列问题:
(1)函数y=f(x)在区间[0.55,0.6]上是否存在零点,写出判断并说明理由;
(2)证明:函数y=f(x)在区间(-∞,-0.35]单调递减.
| x | 3.27 | 1.57 | -0.61 | -0.59 | 0.26 | 0.42 | -0.35 | -0.56 | 4.25 | |
| y | -101.63 | -10.04 | 0.07 | 0.03 | 0.21 | 0.20 | -0.22 | -0.03 | -226.05 |
(1)函数y=f(x)在区间[0.55,0.6]上是否存在零点,写出判断并说明理由;
(2)证明:函数y=f(x)在区间(-∞,-0.35]单调递减.
 =(x,1),
=(x,1), =(-1,b-x),函数f(x)=a-
=(-1,b-x),函数f(x)=a-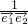 是偶函数.
是偶函数. =(x,1),
=(x,1), =(-1,b-x),函数f(x)=a-
=(-1,b-x),函数f(x)=a- 是偶函数.
是偶函数.