题目内容
已知两点A(3,-4),B(-9,2),在直线AB上求一点P,使|
|=
|
|.
| AP |
| 1 |
| 3 |
| AB |
考点:平面向量的坐标运算
专题:平面向量及应用
分析:设出点P的坐标,由条阿金根据向量之间的关系转化为坐标运算即可,整理出关于所设的向量坐标的方程组,解方程组即可.
解答:
解:设点P(x,y)在直线AB上,∵
=(-12,6),
=(x-3,y+4),|
|=
|
|,
若
=
,则有(x-3,y+4)=(-4,2),求得x=-1,y=-2,点P(-1,2).
若
=-
,则有(x-3,y+4)=(4,-2),求得x=7,y=-6,点P(7,-6).
综上可得,点P(-1,2),或点P(7,-6).
| AB |
| AP |
| AP |
| 1 |
| 3 |
| AB |
若
| AP |
| 1 |
| 3 |
| AB |
若
| AP |
| 1 |
| 3 |
| AB |
综上可得,点P(-1,2),或点P(7,-6).
点评:本题考查向量坐标的运算,考查向量模长转化为向量之间的关系时要注意到问题,本题是一个易错题,容易漏掉一种情况.

练习册系列答案
相关题目
有四个数a1,a2,a3,a4,前三个数成等比,积为64;后三个数成等差,和为6;则a1=( )
| A、9 | B、8 | C、16 | D、4 |
设等比数列{an}的公比为q,前n项和为Sn,若S8,S7,S9成等差数列,则公比q为( )
| A、q=1 |
| B、q=-2或q=1 |
| C、q=-2 |
| D、q=2或q=-1 |
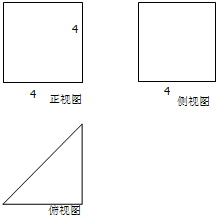 一个几何体的三视图如图所示,则这个几何体的表面积等于
一个几何体的三视图如图所示,则这个几何体的表面积等于