题目内容
若函数f(x)=asinωx+bcosωx(0<ω<5,ab≠0)的图象的一条对称轴方程是x=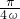 ,函数f′(x)的图象的一个对称中心是(
,函数f′(x)的图象的一个对称中心是( ,0),则f(x)的最小正周期是________.
,0),则f(x)的最小正周期是________.
π
分析:根据两角和与差的正弦公式整理函数,根据对称轴对应的函数值是正负 ,代入数值两边平方,得到a=b,写出函数的导函数,根据导函数的对称中心,得到ω的值,求出最小正周期.
,代入数值两边平方,得到a=b,写出函数的导函数,根据导函数的对称中心,得到ω的值,求出最小正周期.
解答:∵函数f(x)=asinωx+bcosωx= sin(ωx+φ)
sin(ωx+φ)
图象的一条对称轴方程是x=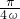 ,
,
∴把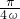 代入,得到
代入,得到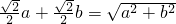
两边平方得到a=b,
∴f(x)=asinωx+acosωx= asin(ωx+
asin(ωx+ )
)
∵函数f′(x)的图象的一个对称中心是( ,0),
,0),
∴f′(x)= aωcos(ωx+
aωcos(ωx+ )过(
)过( ,0),
,0),
∴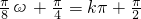 ,
,
又∵0<ω<5,
∴k=0时,ω=2符合题意
∴函数的最小正周期是
故答案为:π
点评:本题主要考查了利用辅助角公式把函数化简为同一个角的三角函数,本题解题的关键是函数的导函数的一个对称中心,代入可以求出ω的值,根据对称轴可以求出a,b相等的条件,本题是一个中档题目.
分析:根据两角和与差的正弦公式整理函数,根据对称轴对应的函数值是正负
 ,代入数值两边平方,得到a=b,写出函数的导函数,根据导函数的对称中心,得到ω的值,求出最小正周期.
,代入数值两边平方,得到a=b,写出函数的导函数,根据导函数的对称中心,得到ω的值,求出最小正周期.解答:∵函数f(x)=asinωx+bcosωx=
 sin(ωx+φ)
sin(ωx+φ)图象的一条对称轴方程是x=
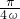 ,
,∴把
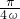 代入,得到
代入,得到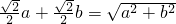
两边平方得到a=b,
∴f(x)=asinωx+acosωx=
 asin(ωx+
asin(ωx+ )
)∵函数f′(x)的图象的一个对称中心是(
 ,0),
,0),∴f′(x)=
 aωcos(ωx+
aωcos(ωx+ )过(
)过( ,0),
,0),∴
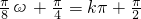 ,
,又∵0<ω<5,
∴k=0时,ω=2符合题意
∴函数的最小正周期是

故答案为:π
点评:本题主要考查了利用辅助角公式把函数化简为同一个角的三角函数,本题解题的关键是函数的导函数的一个对称中心,代入可以求出ω的值,根据对称轴可以求出a,b相等的条件,本题是一个中档题目.

练习册系列答案
 芝麻开花课程新体验系列答案
芝麻开花课程新体验系列答案
相关题目
 (n∈N*)
(n∈N*) .
. 对不小于2的正整数恒成立,求x的取值范围.
对不小于2的正整数恒成立,求x的取值范围.