题目内容
(本小题满分12分)
如图,已知多面体ABCDE中,AB⊥平面ACD,DE⊥平面ACD,AC=AD=CD=DE=2,AB=1,F为CD的中点.
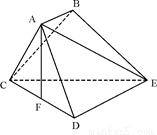
(Ⅰ)求证:AF⊥平面CDE;
(Ⅱ)求面ACD和面BCE所成锐二面角的大小.
【答案】
(1)要证明面面垂直 ,则要通过判定定理,先证明DE⊥平面ACD,AF 平面ACD,∴DE⊥AF,以及AF⊥CD,从而得到证明。
平面ACD,∴DE⊥AF,以及AF⊥CD,从而得到证明。
(2) 45°
【解析】
试题分析:解:(Ⅰ)∵DE⊥平面ACD,AF 平面ACD,∴DE⊥AF.
平面ACD,∴DE⊥AF.
又∵AC=AD,F为CD中点,∴AF⊥CD,
因CD∩DE=D,∴AF⊥平面CDE. ……………… 4分
(Ⅱ)取CE的中点Q,连接FQ,因为F为CD的中点,则FQ∥DE,故DE⊥平面ACD,∴FQ⊥平面ACD,又由(Ⅰ)可知FD,FQ,FA两两垂直,以O为坐标原点,建立如图坐标系,

则F(0,0,0),C( ,0,0),A(0,0,
,0,0),A(0,0, ),B(0,1,
),B(0,1, ),E(1,2,0).
),E(1,2,0).
设面BCE的法向量 ,则
,则
即 取
取 .
.
又平面ACD的一个法向量为 ,
,
∴  .
.
∴面ACD和面BCE所成锐二面角的大小为45°.
考点:空间中二面角和线面垂直的证明
点评:解决的关键是利用线面垂直的判定定理以及二面角的定义来分析求解,属于基础题 。

练习册系列答案
相关题目