题目内容
对于一切实数,当a,b,c(a≠0,a<b)变化时,所有二次函数f(x)=ax2+bx+c的函数值恒为非负实数,则
的最小值是( )
| a+b+c |
| b-a |
分析:由于二次函数的值恒为非负数,推出a>0,故 b>a>0,再由△≤0得到c≥
,化简所求表达式,通过二次函数对应的根的范围,结合韦达定理,求出a的范围即可.
| b2 |
| 4a |
解答:解:由于二次函数的值恒为非负数,可得a>0,故 b>a>0,再由△≤0得到c≥
.
则
≥
=
.
令y=
,则有
•(
) 2+(1-y)
+1+y=0 ①.
∵△≥0,解得 y≥3,或 y≤0.
再由 b>a>0可得
>1,故方程①的两根之和4(y-1)>2,
∴y>
,故舍去y≤0,取y≥3.
即y的最小值为3,
故选B.
| b2 |
| 4a |
则
| a+b+c |
| b-a |
a+b+
| ||
| b-a |
1+
| ||||||
|
令y=
1+
| ||||||
|
| 1 |
| 4 |
| b |
| a |
| b |
| a |
∵△≥0,解得 y≥3,或 y≤0.
再由 b>a>0可得
| b |
| a |
∴y>
| 3 |
| 2 |
即y的最小值为3,
故选B.
点评:本题主要考查二次函数判别式的应用,考查韦达定理的应用,考查计算能力,属于中档题.

练习册系列答案
相关题目
 恒过定点
恒过定点 ,则焦点在y轴上且过点
,则焦点在y轴上且过点 .
. 与直线
与直线 垂直,则实数k=1;
垂直,则实数k=1; 对于任意
对于任意 ,有
,有 ,若
,若 ,则
,则 4
4 ,令
,令 为不大于
为不大于 ,则函数
,则函数 称为高斯函数或取整函数,若
称为高斯函数或取整函数,若 ,
, 为数列
为数列 的前
的前 项和,则
项和,则 145
145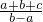 的最小值是
的最小值是

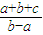 的最小值是( )
的最小值是( )
