题目内容
3. 如图,抛物线关于y轴对称,它的顶点在坐标原点,点P(2,1),
如图,抛物线关于y轴对称,它的顶点在坐标原点,点P(2,1),A(x1,y1),B(x2,y2)均在抛物线上.
(Ⅰ)求抛物线的方程;
(Ⅱ)若∠APB的平分线垂直于y轴,证明直线AB的斜率为定值.
分析 (Ⅰ)设出抛物线方程,再代入点P坐标,即可求得抛物线方程;
(Ⅱ)若∠APB的平分线垂直于y轴,则有kAP+kBP=0,运用直线的斜率公式和点在曲线上满足抛物线方程,化简整理,再由AB的斜率公式,计算即可得到定值.
解答 (Ⅰ)解:设抛物线的方程为x2=2py(p>0),
由点P(2,1)在抛物线上,
即有22=2p,解得p=2,
则有抛物线的方程为x2=4y;
(Ⅱ)证明:若∠APB的平分线垂直于y轴,
则有kAP+kBP=0,
即$\frac{{y}_{1}-1}{{x}_{1}-2}$+$\frac{{y}_{2}-1}{{x}_{2}-2}$=0,
即有$\frac{\frac{{{x}_{1}}^{2}}{4}-1}{{x}_{1}-1}$+$\frac{\frac{{{x}_{2}}^{2}}{4}-1}{{x}_{2}-1}$=0,
化简得,$\frac{1}{4}$(x1+2)+$\frac{1}{4}$(x2+2)=0,
即为x1+x2=-4,
则有kAB=$\frac{{y}_{1}-{y}_{2}}{{x}_{1}-{x}_{2}}$=$\frac{\frac{{{x}_{1}}^{2}}{4}-\frac{{{x}_{2}}^{2}}{4}}{{x}_{1}-{x}_{2}}$=$\frac{1}{4}$(x1+x2)=-1.
点评 本题考查抛物线的方程和性质,主要待定系数法求方程的方法,同时考查直线的斜率公式和对称性的运用,属于中档题.

练习册系列答案
相关题目
12.已知a为实数,则|a|≥1是关于x的绝对值不等式|x|+|x-1|≤a有解的( )
| A. | 充分不必要条件 | B. | 必要不充分条件 | ||
| C. | 充要条件 | D. | 既不充分也不必要条件 |
 是虚数单位,若复数
是虚数单位,若复数 在复平面内对应的点在第四象限,则实数
在复平面内对应的点在第四象限,则实数 的值可以是( )
的值可以是( ) 的值域是
的值域是 ;②
;② 的值域为
的值域为 ;③
;③ 的值域为
的值域为 ;④
;④ 的值域为
的值域为 ,其中错误的命题的个数有( )
,其中错误的命题的个数有( )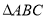 中,
中, ,若
,若 为
为 的值为( )
的值为( ) ,则函数
,则函数 的最小正周期与最大值分别为( )
的最小正周期与最大值分别为( ) B.
B.
 D.
D.