题目内容
12.已知a为实数,则|a|≥1是关于x的绝对值不等式|x|+|x-1|≤a有解的( )| A. | 充分不必要条件 | B. | 必要不充分条件 | ||
| C. | 充要条件 | D. | 既不充分也不必要条件 |
分析 解不等式和不等式的几何意义可得各自对应的a的集合,由集合的包含关系可判.
解答 解:由|a|≥1可得a≤-1或a≥1,
又关于x的绝对值不等式|x|+|x-1|≤a有解,
∴a≥|x|+|x-1|的最小值,
又∵|x|+|x-1|表示数轴上的点到0和1的距离之和,
∴|x|+|x-1|的最小值为1,即a≥1,
∵{a|a≥1}是集合{a|a≤-1或a≥1}的真子集,
∴|a|≥1是关于x的绝对值不等式|x|+|x-1|≤a有解的必要不充分条件,
故选:B
点评 本题考查充要条件的判定,涉及绝对值不等式的恒成立问题,属基础题.

练习册系列答案
相关题目
17.已知平行四边形OABC,$\overrightarrow{OA}$=(4,2),$\overrightarrow{OC}$=(2,6),则$\overrightarrow{OB}$与$\overrightarrow{AC}$夹角的余弦是( )
| A. | $\frac{\sqrt{2}}{2}$ | B. | -$\frac{\sqrt{2}}{2}$ | C. | $\frac{\sqrt{5}}{5}$ | D. | -$\frac{\sqrt{5}}{5}$ |
4.已知x,y∈R,且$\left\{\begin{array}{l}{\sqrt{3}x+y≤4\sqrt{3}}\\{\sqrt{3}x-y≥0}\\{y≥0}\end{array}\right.$,则存在θ∈R,使得xcosθ+ysinθ+1=0成立的P(x,y)构成的区域面积为( )
| A. | 4$\sqrt{3}$-$\frac{π}{6}$ | B. | 4$\sqrt{3}$-$\frac{π}{3}$ | C. | $\frac{π}{2}$ | D. | $\frac{\sqrt{3}}{4}$+$\frac{π}{6}$ |
1.把一根长度为7的铁丝截成3段,如果三段的长度均为正整数,则能构成三角形的概率为( )
| A. | $\frac{1}{4}$ | B. | $\frac{1}{2}$ | C. | $\frac{3}{4}$ | D. | $\frac{1}{3}$ |
 ,求函数的定义域和值域.
,求函数的定义域和值域.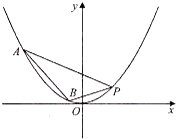 如图,抛物线关于y轴对称,它的顶点在坐标原点,点P(2,1),
如图,抛物线关于y轴对称,它的顶点在坐标原点,点P(2,1),