题目内容
8.斜率为2$\sqrt{2}$的直线l经过抛物线y2=8x的焦点F,且抛物线相交于A、B两点,则线段AB的长为9.分析 求得抛物线的焦点,设出直线l的方程,联立抛物线方程,消去y,解方程求得交点A,B,再由两点的距离公式计算即可得到所求值.
解答 解:抛物线y2=8x的焦点F为(2,0),
则直线l:y=2$\sqrt{2}$(x-2),
代入抛物线方程y2=8x,可得
x2-5x+4=0,
解得x1=1,x2=4,
即有y1=-2$\sqrt{2}$,y2=4$\sqrt{2}$.
即有|AB|=$\sqrt{({x}_{1}-{x}_{2})^{2}+({y}_{1}-{y}_{2})^{2}}$
=$\sqrt{(1-4)^{2}+(-2\sqrt{2}-4\sqrt{2})^{2}}$
=9.
故答案为:9.
点评 本题考查抛物线的方程和性质,主要考查抛物线的方程的运用,注意联立直线方程和抛物线方程,求出交点,运用两点的距离,属于基础题.

练习册系列答案
 云南师大附小一线名师提优作业系列答案
云南师大附小一线名师提优作业系列答案 冲刺100分单元优化练考卷系列答案
冲刺100分单元优化练考卷系列答案
相关题目
13. 如图,一条直线与抛物线y2=2px(p>0)交于A,B两点,且OA⊥OB,F为抛物线的焦点,若△ABO与△AFO面积之和的最小值为50$\sqrt{5}$,则抛物线的方程为( )
如图,一条直线与抛物线y2=2px(p>0)交于A,B两点,且OA⊥OB,F为抛物线的焦点,若△ABO与△AFO面积之和的最小值为50$\sqrt{5}$,则抛物线的方程为( )
 如图,一条直线与抛物线y2=2px(p>0)交于A,B两点,且OA⊥OB,F为抛物线的焦点,若△ABO与△AFO面积之和的最小值为50$\sqrt{5}$,则抛物线的方程为( )
如图,一条直线与抛物线y2=2px(p>0)交于A,B两点,且OA⊥OB,F为抛物线的焦点,若△ABO与△AFO面积之和的最小值为50$\sqrt{5}$,则抛物线的方程为( )| A. | y2=20x | B. | y2=10x | C. | y2=5x | D. | y2=$\frac{5}{2}$x |
17.已知平行四边形OABC,$\overrightarrow{OA}$=(4,2),$\overrightarrow{OC}$=(2,6),则$\overrightarrow{OB}$与$\overrightarrow{AC}$夹角的余弦是( )
| A. | $\frac{\sqrt{2}}{2}$ | B. | -$\frac{\sqrt{2}}{2}$ | C. | $\frac{\sqrt{5}}{5}$ | D. | -$\frac{\sqrt{5}}{5}$ |
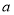 、
、 、
、 是正实数,且
是正实数,且 ,求证:
,求证: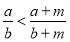 .
. 中,内角
中,内角 的对边分别为
的对边分别为 ,已知
,已知 .
. 的大小;
的大小; ,且
,且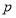 的取值范围.
的取值范围. 为平面向量,若
为平面向量,若 与
与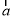 的夹角为
的夹角为 与
与 的夹角为
的夹角为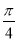 ,则
,则 ( )
( )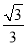 B.
B.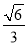
 D.2
D.2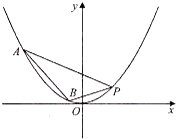 如图,抛物线关于y轴对称,它的顶点在坐标原点,点P(2,1),
如图,抛物线关于y轴对称,它的顶点在坐标原点,点P(2,1),