题目内容
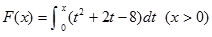 .
.
(1)求 的单调区间;(2)求函数
的单调区间;(2)求函数 在
在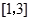 上的最值.
上的最值.
(1)单调增区间是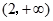 ,单调递减区间是
,单调递减区间是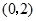 ;(2)最大值是
;(2)最大值是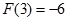 ,最小值是
,最小值是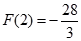 .
.
解析试题分析:(1)首先利用牛顿-莱布尼兹公式求出函数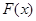 的表达式,并注意题中所给
的表达式,并注意题中所给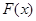 的定义域为
的定义域为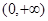 ,再利用导数通过解不等式
,再利用导数通过解不等式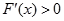 及
及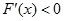 并与定义域取交集而求得函数的单调区间;(2)求函数最值的一般步骤:①求出函数在给定区间上的极值及区间的端点所对应的函数值;②比较上述值的大小;③得结论:其中最大者即为函数的最大值,最小者即为函数的最小值.
并与定义域取交集而求得函数的单调区间;(2)求函数最值的一般步骤:①求出函数在给定区间上的极值及区间的端点所对应的函数值;②比较上述值的大小;③得结论:其中最大者即为函数的最大值,最小者即为函数的最小值.
试题解析:依题意得,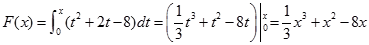 ,定义域是
,定义域是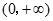 .
.
(1) ,
,
令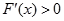 ,得
,得 或
或 ,
,
令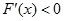 ,得
,得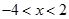
由于定义域是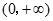 ,
, 函数的单调增区间是
函数的单调增区间是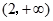 ,单调递减区间是
,单调递减区间是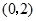 .
.
(2)令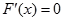 ,得
,得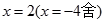 ,
,
由于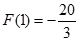 ,
,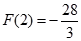 ,
,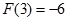 ,
,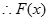 在
在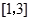 上的最大值是
上的最大值是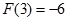 ,最小值是
,最小值是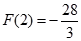 .
.
考点:1.定积分的基本公式;2.函数的单调区间;3.函数的最值.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
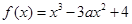 ,其中
,其中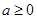 。
。 ,求函数
,求函数 的极值点和极值;
的极值点和极值;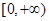 上的最小值。
上的最小值。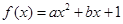 (
( 为实数,
为实数, ),
), ,⑴若
,⑴若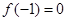 ,且函数
,且函数 的值域为
的值域为 ,求
,求 的表达式;
的表达式; ,且函数
,且函数 是否大0?
是否大0?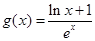 ,当
,当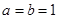 时,证明:对任意实数
时,证明:对任意实数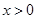 ,
, (其中
(其中 是
是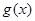 的导函数) .
的导函数) . 满足:①在
满足:①在 时有极值;②图像过点
时有极值;②图像过点 ,且在该点处的切线与直线
,且在该点处的切线与直线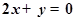 平行.
平行.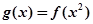 的单调递增区间.
的单调递增区间. 在点
在点 处取得极小值-4,使其导数
处取得极小值-4,使其导数 的
的 的取值范围为
的取值范围为 ,求:
,求: 的解析式;
的解析式; ,求
,求 的最大值;
的最大值;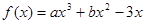 在
在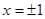 处取得极值,求函数
处取得极值,求函数 以及
以及 ,过点P
,过点P 的直线
的直线 与曲线
与曲线 相切,求
相切,求 ,当
,当 时,
时, 在1,4上的最小值为
在1,4上的最小值为 ,求
,求 在
在 与
与 处都取得极值.
处都取得极值.  ,
, 的值;
的值; ,若对任意的
,若对任意的 ,总存在
,总存在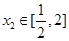 ,使得:
,使得: ,求实数
,求实数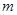 的取值范围.
的取值范围. ,
, .
.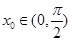 ,使
,使 ;
; ,使
,使 ,且对(1)中的
,且对(1)中的 .
.