题目内容
(本小题满分12分)已知椭圆的一个顶点为A(0,-1),焦点在x轴上.若右焦点到直线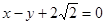 的距离为3.
的距离为3.
(1)求椭圆的方程;
(2)设椭圆与直线 相交于不同的两点M、N.当
相交于不同的两点M、N.当 时,求
时,求 的取值范围.
的取值范围.
【答案】
(1)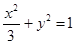 (2)(
(2)(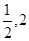 )
)
【解析】
试题分析:(1)依题意可设椭圆方程为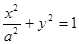 ,则右焦点F(
,则右焦点F(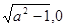 ,
,
由题设可得: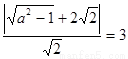 ,解得
,解得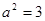 ,
,
故所求椭圆的方程为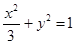 . ……4分
. ……4分
(2)设P为弦MN的中点,由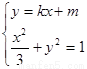 得
得
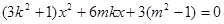 ,
,
由于直线与椭圆有两个交点,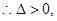 即
即 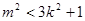 ① ……6分
① ……6分
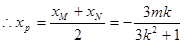 ,从而
,从而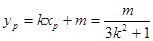 ,
,
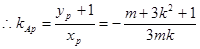 ,
,
又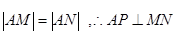 ,
,
则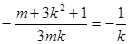 ,即
,即 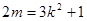 ②
②
把②代入①得 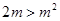 解得
解得
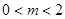 ,
,
由②得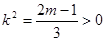 ,解得
,解得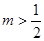 .
.
故所求m的取范围是(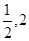 ). ……12分
). ……12分
考点:本小题主要考查椭圆标准方程的求解和直线与椭圆的位置关系、弦长公式以及中点坐标公式、斜率公式等的综合应用,考查学生数形结合解决问题的能力和运算求解能力.
点评:圆锥曲线是每年高考的重点考查内容,涉及到直线与圆锥曲线的位置关系时,运算量比较大,要结合图形,数形结合可以简化运算.

练习册系列答案
 全优点练单元计划系列答案
全优点练单元计划系列答案
相关题目