题目内容
已知函数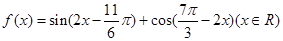 .
.
(1)用“五点法”画出函数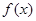 在一个周期内的图像
在一个周期内的图像
(2)求函数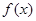 的最小正周期和单调增区间;
的最小正周期和单调增区间;
(3)在区间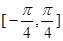 上的最大值和最小值.
上的最大值和最小值.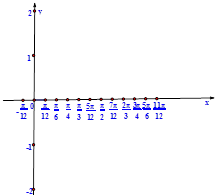
(1)见解析;(2) ,
,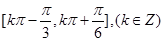 ;(3)2,
;(3)2,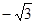 .
.
解析试题分析:(1)用五点法函数y=Asin(ωx+∅)在一个周期上的简图.
(2)由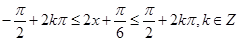 ,求得x的范围,即可求得函数的增区间.
,求得x的范围,即可求得函数的增区间.
(3)根据x的范围,求得角 的范围,再根据正弦函数的定义域和值域求得f(x)的最大值和最小值.
的范围,再根据正弦函数的定义域和值域求得f(x)的最大值和最小值.
(1)由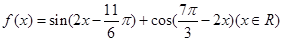 得:
得: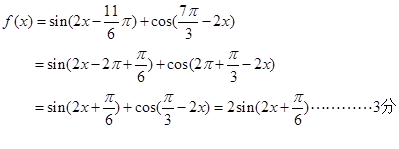
列表如下:
图像如下: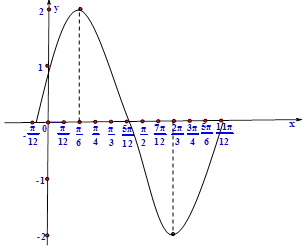
(2)函数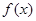 的最小正周期为
的最小正周期为 ,又由
,又由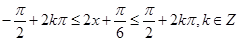 可得
可得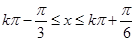
所以函数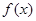 的单调增区间为
的单调增区间为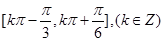
(3)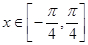 时,
时,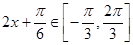 ,当
,当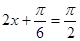 ,即
,即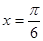 时,
时,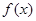 取得最大值为
取得最大值为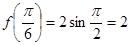 ;当
;当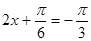 ,即
,即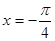 时,
时,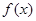 取得最小值为
取得最小值为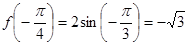 .
.
考点:1、五点法作函数y=Asin(ωx+∅)的简图;2、正弦函数的单调性;3、正弦函数的定义域和值域.

练习册系列答案
 备战中考寒假系列答案
备战中考寒假系列答案
相关题目
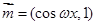 ,
,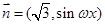 (
(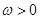 ),函数
),函数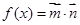 ,且
,且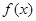 图象上一个最高点为
图象上一个最高点为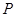
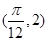 ,与
,与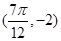 .
. 为常数,判断方程
为常数,判断方程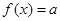 在区间
在区间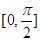 上的解的个数;
上的解的个数;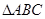 中,若
中,若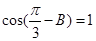 ,求
,求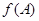 的取值范围.
的取值范围.
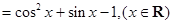 .
.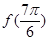 的值;
的值;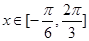 时,求
时,求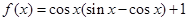 .
. 的最小正周期;
的最小正周期;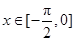 时,求函数
时,求函数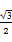 sinωx-sin2
sinωx-sin2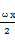 +
+ (ω>0)的最小正周期为π.
(ω>0)的最小正周期为π. 时,求函数f(x)的取值范围.
时,求函数f(x)的取值范围.  的部分图象如图所示.
的部分图象如图所示.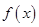 的解析式,并写出
的解析式,并写出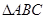 的内角分别是A,B,C,角A为锐角,且
的内角分别是A,B,C,角A为锐角,且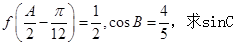 的值.
的值.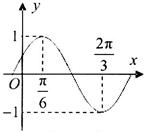
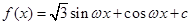 (
( ,
,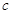 是实数常数)的图像上的一个最高点
是实数常数)的图像上的一个最高点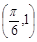 ,与该最高点最近的一个最低点是
,与该最高点最近的一个最低点是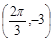 ,
,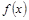 的解析式及其单调增区间;
的解析式及其单调增区间;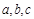 ,且
,且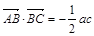 ,角A的取值范围是区间M,当
,角A的取值范围是区间M,当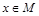 时,试求函数
时,试求函数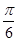 )+1(A>0,ω>0)的最大值为3,其图象相邻两条对称轴之间的距离为
)+1(A>0,ω>0)的最大值为3,其图象相邻两条对称轴之间的距离为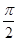 .
.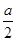 )=2,求α的值.
)=2,求α的值.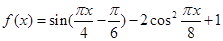 .
. 的最小正周期。
的最小正周期。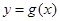 与
与 的图像关于直线
的图像关于直线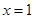 对称,求当
对称,求当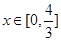 时
时