题目内容
若含有集合A={1,2,4,8,16}中三个元素的A的所有子集依次记为B1,B2,B3,…,Bn(其中n∈N*),又将集合Bi(i=1,2,3,…,n)的元素的和记为ai,则a1+a2+a3+…+an=________.
186
分析:由题意可知集合A中的元素,组成集合A的子集的元素,出现的概率相等,求出每个元素出现的次数,即可求出数列的和.
解答:含有集合A={1,2,4,8,16}中三个元素的A的子集有C53=10个,
这样10个集合中,每个集合中都有3个元素,总计元素出现的次数是30,
A中“1,2,4,8,16”这5个元素出现的几率是一样的,
所以每个元素都出现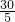 =6次,
=6次,
所以a1+a2+a3+…+an=6×(1+2+4+8+16)=186.
故答案为:186.
点评:本题是中档题,考查数列求和,集合中元素的特征,概率、排列组合等知识,考查计算能力,转化思想.
分析:由题意可知集合A中的元素,组成集合A的子集的元素,出现的概率相等,求出每个元素出现的次数,即可求出数列的和.
解答:含有集合A={1,2,4,8,16}中三个元素的A的子集有C53=10个,
这样10个集合中,每个集合中都有3个元素,总计元素出现的次数是30,
A中“1,2,4,8,16”这5个元素出现的几率是一样的,
所以每个元素都出现
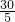 =6次,
=6次,所以a1+a2+a3+…+an=6×(1+2+4+8+16)=186.
故答案为:186.
点评:本题是中档题,考查数列求和,集合中元素的特征,概率、排列组合等知识,考查计算能力,转化思想.

练习册系列答案
相关题目