题目内容
直线l过点(-4,0)且与圆(x+1)2+(y-2)2=25交于A,B两点,如果AB=8,求直线l的方程.
5x+12y+20=0或x+4=0
学生错解:解:设直线l的方程为y=k(x+4),由被圆截得的弦长为8,可得圆心(-1,2)到直线y=k(x+4)的距离为3,即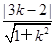 =3,解得k=-
=3,解得k=-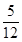 ,此时直线方程为5x+12y+20=0.
,此时直线方程为5x+12y+20=0.
审题引导:(1)如何设过定点的直线的方程?(2)圆中弦长的问题,通常作怎样的辅助线构造直角三角形来解决?
规范解答:解:过点(-4,0)的直线若垂直于x轴,经验证符合条件,即方程为x+4=0满足题意;(4分)
若存在斜率,设其直线方程为y=k(x+4),由被圆截得的弦长为8,可得圆心(-1,2)到直线y=k(x+4)的距离为3,
即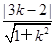 =3,解得k=-
=3,解得k=-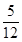 ,(10分)
,(10分)
此时直线方程为5x+12y+20=0,(12分)
综上直线方程为5x+12y+20=0或x+4=0.(14分)
错因分析:1.解答本题易误认为斜率k一定存在从而漏解.2.对于过定点的动直线设方程时,可结合题意或作出符合题意的图形分析斜率k是否存在,以避免漏解.
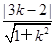 =3,解得k=-
=3,解得k=-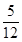 ,此时直线方程为5x+12y+20=0.
,此时直线方程为5x+12y+20=0.审题引导:(1)如何设过定点的直线的方程?(2)圆中弦长的问题,通常作怎样的辅助线构造直角三角形来解决?
规范解答:解:过点(-4,0)的直线若垂直于x轴,经验证符合条件,即方程为x+4=0满足题意;(4分)
若存在斜率,设其直线方程为y=k(x+4),由被圆截得的弦长为8,可得圆心(-1,2)到直线y=k(x+4)的距离为3,
即
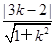 =3,解得k=-
=3,解得k=-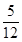 ,(10分)
,(10分)此时直线方程为5x+12y+20=0,(12分)
综上直线方程为5x+12y+20=0或x+4=0.(14分)
错因分析:1.解答本题易误认为斜率k一定存在从而漏解.2.对于过定点的动直线设方程时,可结合题意或作出符合题意的图形分析斜率k是否存在,以避免漏解.

练习册系列答案
相关题目
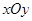 中,圆C的方程为
中,圆C的方程为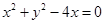 .若直线
.若直线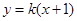 上存在一点
上存在一点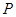 ,使过
,使过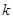 的取值范围是 .
的取值范围是 .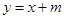 与曲线
与曲线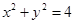 交于不同的两点
交于不同的两点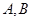 ,若
,若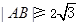 ,则实数
,则实数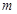 的取值范围是 .
的取值范围是 .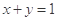 与圆
与圆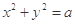 交于
交于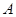 、
、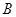 两点,
两点,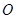 是原点,C是圆上一点,若
是原点,C是圆上一点,若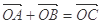 ,则
,则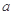 的值为( )
的值为( )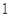
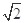
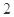
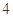
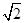 =0上点P作圆x2+y2=1的两条切线,若两条切线的夹角是60°,则点P的坐标是__________.
=0上点P作圆x2+y2=1的两条切线,若两条切线的夹角是60°,则点P的坐标是__________.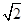 =0上点P作圆x2+y2=1的两条切线,若两条切线的夹角是60°,则点P的坐标是____________.
=0上点P作圆x2+y2=1的两条切线,若两条切线的夹角是60°,则点P的坐标是____________.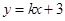 与圆
与圆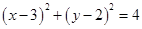 相交于M,N两点,若
相交于M,N两点,若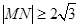 ,则
,则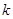 的取值范围是( )
的取值范围是( )


