题目内容
(本小题满分12分)
已知圆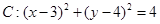 和直线
和直线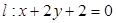 ,直线
,直线 ,
, 都经过圆C外定点A(1,0).
都经过圆C外定点A(1,0).
(Ⅰ)若直线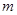 与圆C相切,求直线
与圆C相切,求直线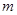 的方程;
的方程;
(Ⅱ)若直线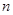 与圆C相交于P,Q两点,与
与圆C相交于P,Q两点,与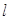 交于N点,且线段PQ的中点为M,
交于N点,且线段PQ的中点为M,
求证: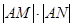 为定值.
为定值.
(Ⅰ)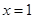 ,
, (Ⅱ)设直线方程为
(Ⅱ)设直线方程为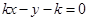 ,由
,由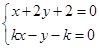 得
得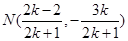 由
由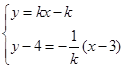 得
得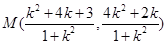
∴ 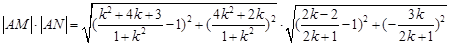
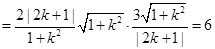 为定值
为定值
解析试题分析:(Ⅰ)①若直线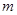 的斜率不存在,即直线是
的斜率不存在,即直线是 ,符合题意. 1分
,符合题意. 1分
②若直线 斜率存在,设直线
斜率存在,设直线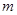 为
为 ,即
,即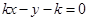 .
.
由题意知,圆心(3,4)到已知直线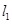 的距离等于半径2,
的距离等于半径2,
即: 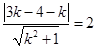 ,解之得
,解之得 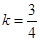 . 5分
. 5分
所求直线方程是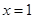 ,
, . 6分
. 6分
(Ⅱ)解法一:直线与圆相交,斜率必定存在,且不为0,
可设直线方程为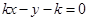
由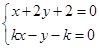 得
得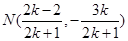 . 8分
. 8分
再由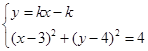
得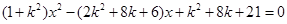 .
.
∴ 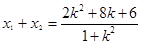 得
得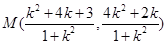 . 12分
. 12分
∴ 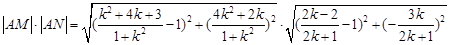
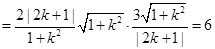 为定值. 14分
为定值. 14分
解法二:直线与圆相交,斜率必定存在,且不为0,可设直线方程为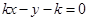
由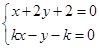 得
得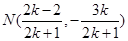 . 8分
. 8分
又直线CM与 垂直,
垂直,
由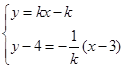 得
得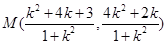 . 10分
. 10分
∴ 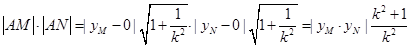
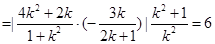 ,为定值. 14分
,为定值. 14分
解法三:用几何法,如图所示,△AMC∽△ABN,则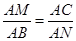 ,
,
可得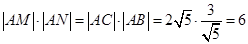 ,是定值.
,是定值.
考点:直线与圆的位置关系
点评:当直线与圆相切时常用圆心到直线的距离等于圆的半径,当直线与圆相交时常用圆心到直线的距离,弦长一半,圆的半径构成的直角三角形三边勾股定理关系;第一问在求直线方程时需注意分直线斜率存在与不存在两种情况讨论,过直线外一点做圆的切线有2条,不要丢解

练习册系列答案
相关题目