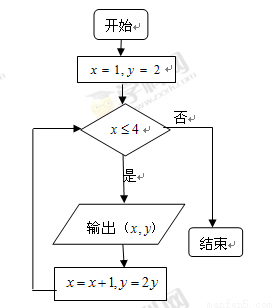
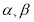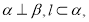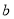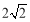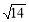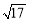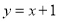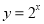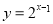题目内容
已知函数f(x)是定义在R上的偶函数,且x≥0时,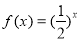 .
.
(1)求f(-1)的值;
(2)求函数f(x)的值域A;
(3)设函数 的定义域为集合B,若A?B,求实数a的取值范围.
的定义域为集合B,若A?B,求实数a的取值范围.
(1) 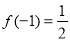 (2)
(2) 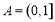 (3)
(3) 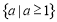
【解析】
试题分析:(1)由函数为偶函数可得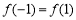 。(2) 函数
。(2) 函数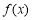 是定义在
是定义在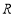 上的偶函数,可得函数
上的偶函数,可得函数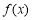 的值域A即为
的值域A即为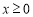 时,
时,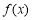 的取值范围.根据指数函数的单调性可求
的取值范围.根据指数函数的单调性可求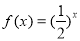 得范围。(3)法一:可先求出集合
得范围。(3)法一:可先求出集合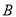 ,根据
,根据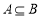 画图分析可得实数
画图分析可得实数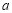 的取值范围。法二:因为
的取值范围。法二:因为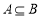 且
且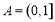 ,所以
,所以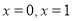 均使
均使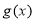 有意义。
有意义。
试题解析:(1)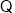 函数
函数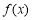 是定义在
是定义在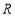 上的偶函数,∴
上的偶函数,∴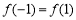 1分
1分
又 x≥0时,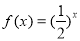 ,
,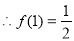 2分
2分
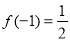 3分
3分
(2)由函数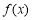 是定义在
是定义在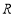 上的偶函数,可得函数
上的偶函数,可得函数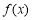 的值域A即为
的值域A即为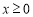 时,
时,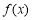 的取值范围 5分
的取值范围 5分
当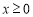 时,
时,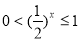 7分
7分
故函数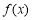 的值域
的值域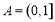 8分
8分
(3)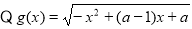
 定义域
定义域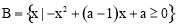 9分
9分
(方法一)由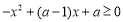 得
得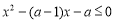 ,
,
即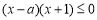 12分
12分
因为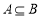 ,∴
,∴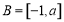 ,且
,且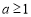 13分
13分
 实数
实数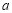 的取值范围是
的取值范围是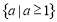 14分
14分
(方法二)设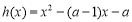
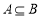 当且仅当
当且仅当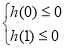 12分
12分
即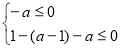 13分
13分
 实数
实数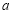 的取值范围是
的取值范围是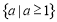 。 14分
。 14分
考点:1函数的奇偶性;2函数的定义域及值域;3指数函数的单调性。