题目内容
设函数 定义域为
定义域为 ,且
,且 .设点
.设点 是函数图像上的任意一点,过点
是函数图像上的任意一点,过点 分别作直线
分别作直线 和
和
 轴的垂线,垂足分别为
轴的垂线,垂足分别为 .
.

(1)写出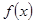 的单调递减区间(不必证明);
的单调递减区间(不必证明);
(2)问: 是否为定值?若是,则求出该定值,若不是,则说明理由;
是否为定值?若是,则求出该定值,若不是,则说明理由;
(3)设 为坐标原点,求四边形
为坐标原点,求四边形 面积的最小值.
面积的最小值.
【答案】
(1)函数 在
在 上是减函数.
上是减函数.
(2)
(3) 。
。
【解析】
试题分析:
思路分析:(1)根据函数 的图象过点
的图象过点 ,确定a,进一步认识函数的单调性。
,确定a,进一步认识函数的单调性。
(2)、设 ,根据直线
,根据直线 的斜率
的斜率 ,确定
,确定 的方程。
的方程。
利用联立方程组求得M,N的坐标,计算可得 。
。
(3)、为求四边形 面积的最小值,根据(2)将面积用
面积的最小值,根据(2)将面积用 表示,
表示,
 ,应用均值定理求解。
,应用均值定理求解。
解:(1)、因为函数 的图象过点
的图象过点 ,
,
所以 函数
函数 在
在 上是减函数.
上是减函数.
(2)、设 ,直线
,直线 的斜率
的斜率 ,
,
则 的方程
的方程 。
。
联立 ,
,
 、
、
 ,
,

(2)、(文)设 ,直线
,直线 的斜率为
的斜率为 ,
,
则 的方程
的方程 ,
,
联立 ,
, ,
,
3、  ,
, ,
,
∴ ,
,
 ,
, ,
,
∴  ,
, ,
,
当且仅当 时,等号成立,∴ 此时四边形
时,等号成立,∴ 此时四边形 面积有最小值
面积有最小值 。
。
考点:函数的单调性,直线与双曲线的位置关系,平面向量的坐标运算,均值定理的应用,面积计算。
点评:中档题,本题综合性较强,难度较大。以“对号函数”为背景,综合考查函数的单调性,直线与双曲线的位置关系,平面向量的坐标运算,均值定理的应用,面积计算等。

练习册系列答案
相关题目
 定义域为
定义域为 ,且
,且 .
. 是函数图像上的任意一点,过点
是函数图像上的任意一点,过点 和
和 轴的垂线,垂足分别为
轴的垂线,垂足分别为 .
.
 的单调递减区间(不必证明);(4分)
的单调递减区间(不必证明);(4分) ,求
,求 点的坐标(用
点的坐标(用 为坐标原点,求四边形
为坐标原点,求四边形 面积的最小值.(7分)
面积的最小值.(7分) 定义域为
定义域为 ,且
,且 .
. 是函数图像上的任意一点,过点
是函数图像上的任意一点,过点 和
和 轴的垂线,垂足分别为
轴的垂线,垂足分别为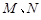 .
.
 的单调递减区间(不必证明);(4分)
的单调递减区间(不必证明);(4分)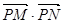 是否为定值?若是,则求出该定值,若不是,则说明理由;(7分)
是否为定值?若是,则求出该定值,若不是,则说明理由;(7分) 为坐标原点,求四边形
为坐标原点,求四边形 面积的最小值.(7分)
面积的最小值.(7分) 设函数
设函数