题目内容
已知x1>0,x1≠1,且xn+1=
,(n=1,2,…).试证:数列{xn}或者对任意自然数n都满足xn<xn+1,或者对任意自然数n都满足xn>xn+1.
xn(
| ||
3
|
证:首先,xn+1-xn=
-xn=
,
由于x1>0,由数列{xn}的定义可知xn>0,(n=1,2,…)
所以,xn+1-xn与1-xn2的符号相同.
①假定x1<1,我们用数学归纳法证明1-xn2>0(n∈N)
显然,n=1时,1-x12>0
设n=k时1-xk2>0,那么当n=k+1时
1-
=1-[
]2=
>0,
因此,对一切自然数n都有1-xn2>0,
从而对一切自然数n都有xn<xn+1
②若x1>1,
当n=1时,1-x12<0;
设n=k时1-xk2<0,那么当n=k+1时
1-
=1-[
]2=
<0,
因此,对一切自然数n都有1-xn2<0,
从而对一切自然数n都有xn>xn+1
xn(
| ||
3
|
2xn(1-
| ||
3
|
由于x1>0,由数列{xn}的定义可知xn>0,(n=1,2,…)
所以,xn+1-xn与1-xn2的符号相同.
①假定x1<1,我们用数学归纳法证明1-xn2>0(n∈N)
显然,n=1时,1-x12>0
设n=k时1-xk2>0,那么当n=k+1时
1-
| x | 2k+1 |
xk(
| ||
3
|
(1-
| ||
(3
|
因此,对一切自然数n都有1-xn2>0,
从而对一切自然数n都有xn<xn+1
②若x1>1,
当n=1时,1-x12<0;
设n=k时1-xk2<0,那么当n=k+1时
1-
| x | 2k+1 |
xk(
| ||
3
|
(1-
| ||
(3
|
因此,对一切自然数n都有1-xn2<0,
从而对一切自然数n都有xn>xn+1

练习册系列答案
相关题目
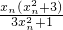 (n=1,2,…)试证:xn<xn+1或xn>xn+1(n=1,2,…).
(n=1,2,…)试证:xn<xn+1或xn>xn+1(n=1,2,…). (n=1,2,…)试证:xn<xn+1或xn>xn+1(n=1,2,…).
(n=1,2,…)试证:xn<xn+1或xn>xn+1(n=1,2,…).