题目内容
已知x1＞0，x1≠1且xn+1=
（n=1，2，…）试证：xn＜xn+1或xn＞xn+1（n=1，2，…）．
【答案】分析：由x1＞0，x1≠1且xn+1=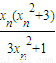
可知xn＞0，所以可用作商比较．
解答：证明∵x1＞0，x1≠1且xn+1=
∴xn＞0
又∵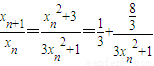
在（0，ω）上是减函数
当
∴xn＞xn+1
当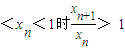
∴xn＜xn+1
点评：本题主要考查数列是递增数列还是递减数列，判断时一般是用比较法．
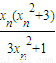可知xn＞0，所以可用作商比较．解答：证明∵x1＞0，x1≠1且xn+1=
∴xn＞0
又∵
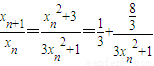在（0，ω）上是减函数当
∴xn＞xn+1
当
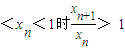
∴xn＜xn+1
点评：本题主要考查数列是递增数列还是递减数列，判断时一般是用比较法．
练习册系列答案
相关题目
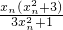（n=1，2，…）试证：xn＜xn+1或xn＞xn+1（n=1，2，…）．