题目内容
(文)已知函数f(x)=(
sinωx+cosωx)cosωx-
(ω>0)的最小正周期为4π.
(1)求ω的值;
(2)求f(x)的单调递增区间.
| 3 |
| 1 |
| 2 |
(1)求ω的值;
(2)求f(x)的单调递增区间.
(1)∵f(x)=
sinωxcosωx+cos2ωx-
=
sin2ωx+
cos2ωx+
-
=sin(2ωx+
),
∵T=
=4π,
∴ω=
.
(2)∵f(x)=sin(
x+
)
∵-
+2kπ≤
x+
≤
+2kπ,k∈Z
∴-
π+4kπ≤x≤
π+4kπ,k∈Z
∴f(x)的单调递增区间为[-
+4kπ,
+4kπ](k∈Z).
| 3 |
| 1 |
| 2 |
=
| ||
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
=sin(2ωx+
| π |
| 6 |
∵T=
| 2π |
| 2ω |
∴ω=
| 1 |
| 4 |
(2)∵f(x)=sin(
| 1 |
| 2 |
| π |
| 6 |
∵-
| π |
| 2 |
| 1 |
| 2 |
| π |
| 6 |
| π |
| 2 |
∴-
| 4 |
| 3 |
| 2 |
| 3 |
∴f(x)的单调递增区间为[-
| 4π |
| 3 |
| 2π |
| 3 |

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
 ,
, ,函数
,函数 ,
,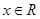 .
.
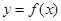 的图像的对称中心坐标;
的图像的对称中心坐标; 个单位,再向左平移
个单位,再向左平移 个单位得函数
个单位得函数 的图像,试写出
的图像,试写出 上的图像.
上的图像. ,使
,使 ; ②函数
; ②函数 是偶函数;
是偶函数;  是函数
是函数 的一条对称轴的方程;
的一条对称轴的方程; 是第一象限的角,且
是第一象限的角,且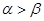 ,则
,则 .
.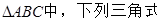 ①sin(A+B)+sinC;②cos(B+C)+cosA;③
①sin(A+B)+sinC;②cos(B+C)+cosA;③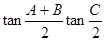
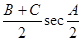 ,其中恒为定值的是 ( )
,其中恒为定值的是 ( )