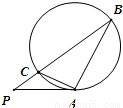题目内容
如图，P为圆O外一点，由P引圆O的切线PA与圆O切于A点，引圆O的割线PB与圆O交于C点．已知AB⊥AC，PA=2，PC=1，则圆O的面积为 ．
【答案】分析：利用切割线定理求出PB，推出BC，求出圆的半径，得到圆的面积．
解答：解：由题意可知PB经过圆的圆心，所以BC 是圆的直径，
由切割线定理的可得PC•PB=PA2，所以PB=4，BC=3，
所以圆的半径为：
，
所以圆O的面积为：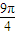
．
故答案为：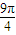
．
点评：本题考查切割线定理与圆的面积的求法与应用，考查计算能力．
解答：解：由题意可知PB经过圆的圆心，所以BC 是圆的直径，
由切割线定理的可得PC•PB=PA2，所以PB=4，BC=3，
所以圆的半径为：
，所以圆O的面积为：
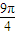．故答案为：
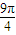．点评：本题考查切割线定理与圆的面积的求法与应用，考查计算能力．
练习册系列答案
金牌教辅培优优选卷期末冲刺100分系列答案
相关题目
选做题：请考生在下列两题中任选一题作答，若两题都做，则按所做的第一题评阅计分．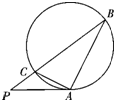
（2012•佛山一模）如图，P为圆O外一点，由P引圆O的切线PA与圆O切于A点，引圆O的割线PB与圆O交于C点．已知AB⊥AC，PA=2，PC=1，则圆O的面积为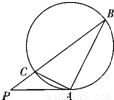
）=
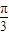，则点M（1，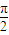
）到直线l的距离为 ．
